Расстояние от точки до точки: формулы, примеры, решения

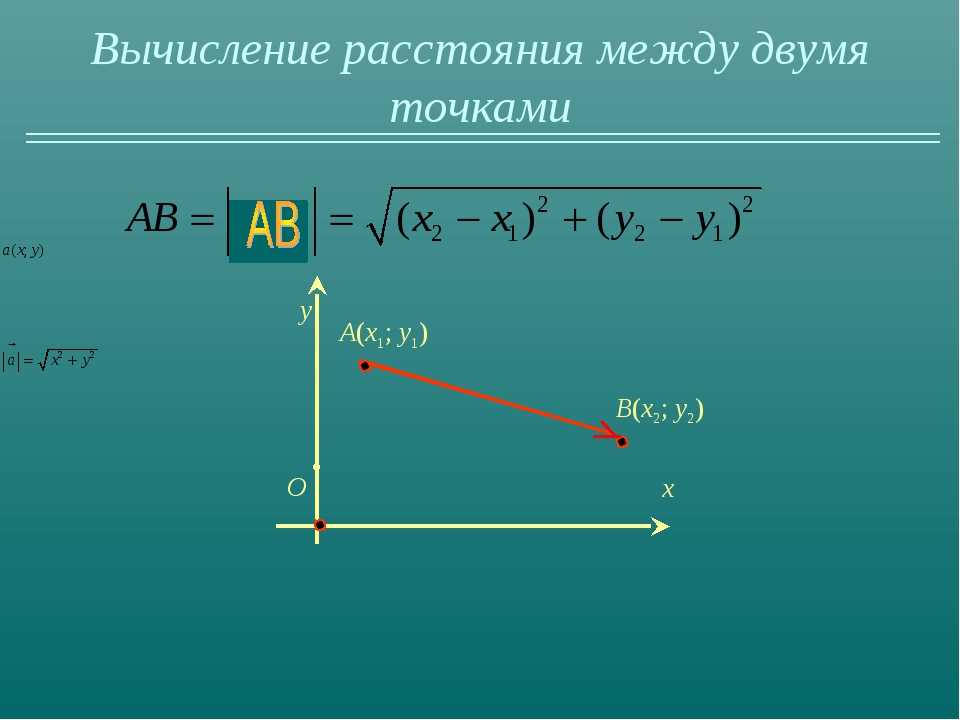
Примеры решения задач на нахождение расстояния между точками

Пример 1

Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A(1-2) и B(11+2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B.

Решение

1. Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно OA=1-2=2-1
2. Расстояние между точками A и B определим как модуль разности координат этих точек: AB=11+2-(1-2)=10+22

Ответ: OA=2-1, AB=10+22

Пример 2

Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней   A(1, -1) и B (λ+1, 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние АВ будет равно 5.

Решение

Чтобы найти расстояние между точками A и B, необходимо использовать формулу AB=(xB-xA)2+yB-yA2

Подставив реальные значения координат, получим:AB=(λ+1-1)2+(3-(-1))2=λ2+16

А также используем имеющееся условие, что АВ=5 и тогда будет верным равенство:

λ2+16=5λ2+16=25λ=±3

Ответ:  АВ = 5, если λ=±3 .

Пример 3

Исходные данные: задано трехмерное пространство в прямоугольной системе координат Oxyz и лежащие в нем точки  A (1, 2, 3) и B-7, -2, 4 .

Решение

 Для решения задачи используем формулу AB=xB-xA2+yB-yA2+(zB-zA)2

Подставив реальные значения, получим: AB=(-7-1)2+(-2-2)2+(4-3)2=81=9 

Ответ: |АВ| = 9

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Система координат

Прежде чем говорить о расстоянии между точками по координатам, следует ввести систему отчета, в которой каждый геометрический объект можно будет однозначно определять. Для этой цели часто используют декартову систему координат. Она представляет собой взаимно перпендикулярные прямые, на каждой из которых отмечены единичные отрезки. Именно в них определяется положение тел в пространстве, на плоскости или на прямой линии.

Для названных трех случаев декартова система координат отличается количеством осей:

• 3 для определения положения пространственных объектов;
• 2 для фигур на плоскости;
• 1 для вычисления координат точек.

Единичные отрезки на координатных осях в общем случае могут иметь разную длину.

Расстояние между точками в пространстве

Исходные данные: прямоугольная система координат Oxyz с лежащими на ней произвольными точками с заданными координатами A(xA, yA, zA) и B(xB, yB, zB) . Необходимо определить расстояние между этими точками.

Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay,  Az, Bx, By, Bz

Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz

Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2

Используя полученные ранее выводы, запишем следующее:

AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA

Преобразуем выражение:

AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2

Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:

AB=xB-xA2+yB-yA2+(zB-zA)2

Полученная формула действительна также для случаев, когда:

— точки совпадают;

— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.

Расстояние между Q и прямой

Полученные знания можно с легкостью применять для решения разнообразных задач по геометрии. Часто приходится находить дистанцию между точкой и прямой. Определить эту величину можно, если знать направляющий вектор прямой. Предположим, что он имеет следующие координаты: a- (x1; y1). Прямая проходит через A (x2; y2). Точка задается так: Q (x0; y0).

В параметрическом виде прямая записывается следующим образом:

Здесь t — параметр, который может принимать любое действительное число. Это выражение позволяет записать равенство (1):

Пусть точка P (x;y) является проекцией Q (x0;y0) на прямую, тогда расстояние PQ является искомой дистанцией, которую следует найти по условию задачи. Поскольку вектора PQ- и a- перпендикулярны друг другу, их скалярное произведение будет равно нулю (угол между векторами равен 90 градусов, его косинус равен нулю). Исходя из этих рассуждений, можно записать выражение (2):

Поскольку имеющиеся равенства (1) и (2) содержат 2 неизвестные переменные, объединение их в систему и решение ее позволит определить точку P (x;y). Зная ее координаты и используя формулу дистанции между двумя точками на плоскости, можно получить искомое расстояние PQ.

Расстояние между точками в пространстве, формула.

Введем прямоугольную систему координат Оxyz в пространстве. Получим формулу для нахождения расстояния от точки до точки .

В общем случае, точки А и В не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки А и В плоскости, перпендикулярные координатным осям Ох, Оу и Oz. Точки пересечения этих плоскостей с координатными осями дадут нам проекции точек А и В на эти оси. Обозначим проекции .

Искомое расстояние между точками А и В представляет собой диагональ прямоугольного параллелепипеда, изображенного на рисунке. По построению, измерения этого параллелепипеда равны и . В курсе геометрии средней школы было доказано, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений, поэтому, . Опираясь на информацию первого раздела этой статьи, мы можем записать следующие равенства , следовательно,
откуда получаем формулу для нахождения расстояния между точками в пространстве .

Эта формула также справедлива, если точки А и В

• совпадают;
• принадлежат одной из координатных осей или прямой, параллельной одной из координатных осей;
• принадлежат одной из координатных плоскостей или плоскости, параллельной одной из координатных плоскостей.

Ломаная линия

Определение

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

Вершинами ломаной линии называются концы отрезков, из которых она состоит.Звеньями ломаной линии называются составляющие ее отрезки.Смежные звенья – это звенья, которые имеют общие вершины.Смежные звенья принадлежать одной прямой.Длина ломаной линии – это сумма длин всех входящих в ее состав звеньев.

На рисунке 12 видно, что:

• KLMN – ломаная линия;
• K, L, M, N – вершины ломаной KLMN;
• KL, LM, MN – звенья ломаной KLMN;
• KL и LM – смежные звенья;
• LM и MN – смежные звенья;
• KL и MN – не являются смежными звеньями.

Называют ломаную линию по названию ее вершин, соблюдая их последовательность. Так, называть ломаную на рисунке 11 как KLMN или NMLK– , а MLKN или MNLK – .

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Название разомкнутой ломаной начинается с названия вершины, с которой она начинается. Замкнутую ломаную можно называть, начиная с любой ее вершины.

На рисунке 12:

• ABCDE
  — замкнутая ломаная;
• FGHKLM
  — разомкнутая ломаная

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя
бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

На рисунке 13 у замкнутой ломаной ABCD два пересекающихся звена: BC ∩DA, а у разомкнутой ломаной EFGHI – три: EF ∩HI и FG ∩HI.

Пример задачи

Применить полученные знания поможет простая геометрическая проблема. Имеется прямая, которая задана на плоскости в виде следующего общего выражения:

Пусть проекцией точки Q на прямую будет нульмерный объект P (x;y). Координаты P должны удовлетворять записанному уравнению.

Чтобы определить направляющий вектор, достаточно взять 2 любые точки на прямой. Подставляя в выражение произвольные значения x, можно определить эти точки A, B и вместе с ними направляющий вектор AB-:

Вектор QP-, который пересекает прямую под прямым углом, должен подчиняться следующему уравнению (свойство скалярного произведения):

В это выражение нужно подставить значение y из уравнения прямой.

Получается:

Таким образом, значение координат проекции Q на прямую равны: P (1,1; -2,3). Остается применить формулу для дистанции между P и Q, чтобы получить ответ на поставленную задачу:

Рассчитанное значение округлено до сотых долей и выражается в единицах единичных векторов координатной системы.

При решении подобных задач для сокращения последующих вычислений рекомендуется проверять принадлежность точки прямой, для чего следует подставить координаты в уравнение. Если этот факт подтверждается, искомое расстояние равно нулю.

Расстояние между точками на координатной прямой

Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.

В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.

К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.

Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.

Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна  11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то OA=xA (число принимается за расстояние); если координата меньше нуля, то OA=-xA . В общем, эти утверждения справедливы для любого действительного числа xA.

Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:

0, если точка совпадает с началом координат;

xA , если xA>0;

-xA , если xA

При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA

Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.

Формула дистанции

Имея полученные представления и знания о свойствах точек и векторов, можно перейти к вопросу нахождения формулы расстояния. Согласно геометрическому определению, под дистанцией между двумя точками понимают длину отрезка, который их соединяет. Эта величина также равна модулю вектора, построенного на нульмерных объектах.

Длину направленного отрезка на плоскости определить просто: необходимо возвести в квадрат каждую его координату, сложить полученные значения, и взять квадратный корень из результирующей суммы. Для вектора a- (x; y) длина будет равна следующей величине:

Возведение суммы в степень 0,5 эквивалентно взятию из нее квадратного корня.

Поскольку определение координат вектора по соответствующим значениям точек известно, можно получить следующую простую формулу для A (x1; y1) и B (x2; y2):

В трехмерном пространстве соответствующее выражение будет иметь подобную форму, только добавится третья координата z.

Коллинеарность векторов

Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что

Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:

Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю

Например, пусть

В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами {0; 0; 0}. Он условно признается коллинеарным любому вектору.

Задание. Выясните, какие из этих пар векторов коллинеарны:

Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:

Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.

Повторяем эти действия в задании б):

На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.

В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.

В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:

Коэффициент k получился одинаковым, поэтому вектора коллинеарны.

В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.

Ответ: а) да; б) нет; в) нет; г) да; д) да.

Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).

Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.

Сначала вычислим коорд-ты векторов АВ и ВС:

Теперь проверяем, коллинеарны ли эти вектора:

Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.

Универсальный способ

Речь идет о координатном представлении нульмерных, одномерных, двумерных и трехмерных геометрических фигур. Параметры точек, треугольников, квадратов, прямых, плоскостей и других более сложных объектов могут быть однозначно выражены в виде наборов чисел, привязанных к соответствующей координатной системе. Поскольку существует задача определения расстояния от точки до точки по координатам, имеет смысл рассмотреть только указанный одномерный объект и вектор.

Точка на плоскости

Этот объект является нульмерным. Для его однозначного определения достаточно знать всего один числовой набор, привязанный к координатной системе. На плоскости имеется всего 2 перпендикулярные оси x и y, поэтому всякая точка будет иметь 2 координаты. Например, A (3; 2), B (-1; 4), C (0; -2), D (0; 0). Первое число здесь означает количество единичных отрезков, которые необходимо отсечь на оси x, второе значение — на оси y. Точка D лежит в начале координат, то есть на пересечении x и y.

В общем случае удобно обозначить произвольную точку Q (x0; y0).

Направленный отрезок в двумерном пространстве

На плоскости координаты направленного отрезка так же, как и точки, представляют собой набор двух чисел. Оба обозначают число отрезков единичной длины, которые следует отложить на каждой оси, чтобы получить проекции вектора на x и y. Например, данные a-(1;-2) означают, что для получения a- следует отложить отрезок 1*i- на оси x и -2*j- на y (два единичных j- в отрицательном направлении оси y). На пересечении этих проекций будет находиться конец a-. Начало его лежит в точке (0; 0).

На плоскости и в трехмерном пространстве всего 2 точки однозначно определяют направленный отрезок. Если его начало переместить в пересечение осей x и y, его конец легко можно найти, вычитая соответствующие координаты точек друг из друга. Следующий простой пример демонстрирует сказанное.

Даны точки A (x1; y1), B (x2; y2), тогда AB- будет иметь координаты:

Вторая точка показывает место расположения конца AB-.

Расстояние между двумя точками на прямой

Пусть заданы на оси OX точки A с координатой x_a и B с координатой x_b (Рис.1). Найдем расстояние между точками A и B.

Расстояние между точками A и В равно:

Поскольку расстояние от O до В равна x_b, а расстояние от O до A равна x_a, получим:

На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:

Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:

На рисунке 3 точки A и В находятся c левой стороны начала координат O.

B этом случае рассояние между точками A и B равно:

Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:

Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).

Формулы (2),(4),(6) можно записать и так:

Пример 1. на оси Ox заданы точки \( \small A(x_a)=A(-4) \) и \( \small B(x_b)=B(7) \) . Найти рассояние между этими точками.

Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):

Ответ: 11.

Расстояние между двумя точками на координатной прямой.

Давайте для начала определимся с обозначениями. Расстояние от точки А до точки В будем обозначать как .

Пусть задана координатная прямая Ox (точка О – начало отсчета) и некоторая точка А на ней. Мы знаем, что каждой точке на координатной прямой соответствует единственное действительное число. Пусть точке А соответствует действительное число , то есть, точка А имеет координату .

Как же определяется расстояние от начала отсчета до точки А? Вообще, измерение расстояния основано на сравнении отрезков — отрезка, соответствующего измеряемому расстоянию от точки до точки, и отрезка, принятого за единицу измерения.

Для точки А, которой соответствует целое число, все очень просто. Мы от точки О вдоль прямой OA последовательно откладываем единичные отрезки, пока не попадем в точку А. Количество единичных отрезков и дает нам расстояние между точками О и А.

Это достаточно очевидно. К примеру, чтобы попасть в точку А, которой соответствует число 2, нам нужно преодолеть расстояние в две единицы от начала отсчета в положительном направлении. Если точка А имеет координату -5, то нам придется отложить один за другим пять единичных отрезков в отрицательном направлении. То есть, в первом случае расстояние равно двум, а во втором случае расстояние от точки О до точки А равно пяти.

Если точке А соответствует рациональное число, то мы можем попасть из начала координат в точку А при помощи последовательного откладывания некоторого количества целых единичных отрезков и его части.

К примеру, если точка А имеет координату , то нам придется отложить один целый единичный отрезок в отрицательном направлении и еще половину от единичного отрезка. В этом случае расстояние равно . Следует отметить, что геометрическими построениями далеко не всегда можно разбить единичный отрезок на необходимое количество частей (например, попробуйте получить единичного отрезка).

Еще интереснее обстоит дело с определением расстояния от точки О до точки А, которой соответствует иррациональное число. К примеру, пусть точке А соответствует число . С помощью откладывания единичного отрезка и его частей от начала отсчета попасть в эту точку не так то просто. В этом случае прибегаем к абстракции: если координата точки А является положительным числом (), то это число принимаем в качестве расстояния, то есть , если же координата точки А есть отрицательное число (), то .

Очевидно, что последнее утверждение справедливо для любого действительного числа .

Итак, расстояние от начала отсчета до точки А, которой соответствует действительное число на координатной прямой, равно

• , если точка А совпадает с началом координат;
• , если ;
• , если .

С помощью знака модуля расстояние от точки О до точки А с координатой можно записать как (смотрите статью модуль числа).

Отсюда можно заключить, что расстояние от точки А с координатой до точки В с координатой равно модулю разности координат, то есть, при любом расположении точек на координатной прямой.

Расстояние между точками на плоскости

Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB) .

Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:

— если точки А и В совпадают, то расстояние между ними равно нулю;

— если точки А и В лежат на прямой, перпендикулярной оси Ox (оси абсцисс), то точки и совпадают, а |АВ| = |АyBy|. Поскольку, расстояние между точками равно модулю разности их координат, то AyBy=yB-yA , а, следовательно AB=AyBy=yB-yA.

— если точки A и B лежат на прямой, перпендикулярной оси Oy (оси ординат) – по аналогии с предыдущим пунктом: AB=AxBx=xB-xA

— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:

Мы видим, что треугольник АВС  является прямоугольным по построению. При этом AC=AxBx и BC=AyBy. Используя теорему Пифагора, составим равенство: AB2=AC2+BC2⇔AB2=AxBx2+AyBy2 , а затем преобразуем его: AB=AxBx2+AyBy2=xB-xA2+yB-yA2=(xB-xA)2+(yB-yA)2

Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек

AB=(xB-xA)2+(yB-yA)2

Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=2+2=

Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:

AB=(xB-xA)2+(yB-yA)2=2+(yB-yA)2=yB-yA

Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:

AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+2=xB-xA

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

С помощью онлайн-карт

Используйте яндекс или гугл карты, чтобы нарисовать и измерить свой пешеходный маршрут.

Зная точное расстояние между точками А и Б, нужно пройти его со своей привычной скоростью, считая шаги. И в конце разделить расстояние на получившееся количество.

Например, проходя стометровку за 150 шагов, мы имеем: 100 / 150 = 0,67 м = 67 см – средняя длина вашего шага. Для интереса сравните потом результат с показаниями вашего шагомера.

Также вы можете использовать на своем мобильном телефоне приложения для ходьбы на основе GPS, но они зачастую показывают на 10% меньше по сравнению с другими вариантами измерения.

Нахождение расстояния от точки до точки, примеры и решения.

Итак, мы получили формулы для нахождения расстояния между двумя точками координатной прямой, плоскости и трехмерного пространства. Пришло время рассмотреть решения характерных примеров.

Число задач, при решении которых конечным этапом является нахождение расстояния между двумя точками по их координатам, поистине огромно. Полный обзор таких примеров выходит за рамки данной статьи. Здесь мы ограничимся примерами, в которых известны координаты двух точек и требуется вычислить расстояние между ними.

Пример.

На координатной прямой Ох заданы две точки и . Найдите расстояние от начала отсчета до точки А, а также расстояние между точками А и В.

Решение.

Расстояние от начала отсчета до точки А на координатной прямой равно модулю координаты этой точки, поэтому, .

Расстояние между двумя точками равно модулю разности их координат: .

Ответ:

.

Пример.

В прямоугольной декартовой системе координат на плоскости заданы две точки и , где — некоторое действительное число. Найдите все значения , при которых расстояние между точками А и В равно 5 единицам.

Решение.

Расстояние от точки А до точки В по их координатам можно найти по формуле . Подставляем координаты: . С другой стороны по условию . Таким образом, значения находим из уравнения :

Ответ:

расстояние между точками А и В равно 5 при .

Пример.

В трехмерном пространстве заданы координаты двух точек и . Найдите расстояние между ними.

Решение.

Для вычисления расстояния от точки А до точки В по координатам воспользуемся формулой :

Ответ:

расстояние между точками равно девяти.

Список литературы.

• Мордкович А.Г. Алгебра. 7 класс. Часть 1: учебник для учащихся общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.

Некогда разбираться?