Как найти ширину прямоугольника ~ инструкции на все случаи жизни

Свойства и линии

Из-за того, что прямоугольник — это параллелограмм, все свойства последнего справедливы и к нему. В первую очередь для него характерно, что противоположные стороны являются параллельными, то есть лежат на непересекающихся прямых. Отсюда следует, что фигуры отличаются друг от друга только размерами двух граней.

К основным свойствам прямоугольника относят:

противолежащие стороны имеют равную длину: AB = CD, BC = AD;
все углы равны 90 градусов;
отрезки, обозначающие ширину и длину, всегда перпендикулярные друг другу: AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB;
сумма любых двух углов фигуры равняется 180 градусов, соответственно всех четырёх — 360;
в четырёхугольном теле можно провести 2 диагонали, длины которых будут совпадать по величине: AB = BC;
сумма квадратов диагональных отрезков равняется удвоенной сумме квадратов сторон фигуры: AC2 + BD2 = 2 (AB2 + BC2);
построенная диагональ разделяет прямоугольник на 2 одинаковые фигуры — прямоугольные треугольники;
точка пересечения прямых линий, соединяющая попарно противоположные углы, является центром фигуры и описанной окружности;
диагонали в месте пересечения разделяются на 4 равных отрезка;
в многоугольник, у которого длина не равна ширине, вписать окружность нельзя, поэтому её можно построить только для частных случаев прямоугольника.

На свойстве, что сложенные квадраты диагоналей можно найти как сумму квадратов всех его сторон, построено решение многих геометрических задач. Нелишним будет доказательство теоремы. Пусть имеется прямоугольник, у которого линии AC и BD — диагонали. Если изобразить многоугольник на рисунке и построить отрезки, можно увидеть, что каждая диагональ делит фигуру на 2 треугольника: ABC и BDC.

Используя теорему косинусов, можно записать: AC2 = AB2 + BC2 — 2 * AB * BC * cos (ABC); BD2 = CD2 + BC2 — 2 * CD * BC * cos (BCD). После сложения полученных выражений получится запись: AC2 + BD2 = AB2 + BC2 — 2 * AB * BC * cos (ABC) + CD2 + BC2 — 2 * CD * BC * cos (BCD).

Так как по свойству прямоугольной фигуры противоположные стороны равны, уравнение примет вид: AC2 + BD2 = 2AB2 + 2BC2 — 2 * AB * BC * cos (ABC) — 2 * AB * BC * cos (BCD). Учитывая, что сумма двух углов равняется 180, полученное выражение можно переписать так: AC2 + BD 2 = 2 (AB 2 + BC 2). Что и следовало доказать.

Алгоритм решение задач с прямой и обратной пропорциональной зависимостью

Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:

Обозначить буквой значение неизвестной величины (чаще всего для этого выбирают латинскую букву Х)
Проанализировать задачу и кратко записать ее условия (краткую запись можно делать в виде таблицы или изображать в виде логической схемы)
Установить зависимость между величинами
В краткой записи задачи обозначить стрелками пропорциональную зависимость

— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин

— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.

5. Записать пропорцию, учитывая характер пропорциональности величин

6. Составить уравнение

7. Найти неизвестный член уравнения (искомую величину)

8. Записать ответ задачи

Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом. Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи

Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.

Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.

Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.

При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.

Пройти тест и получить оценку можно после входа или регистрации

В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.

Формулы прямоугольника:

Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.

Формула стороны прямоугольника (длины и ширины прямоугольника):

Формула диагонали прямоугольника:

d = 2R.

Формулы периметра прямоугольника:

P = 2a + 2b,

P = 2(a + b).

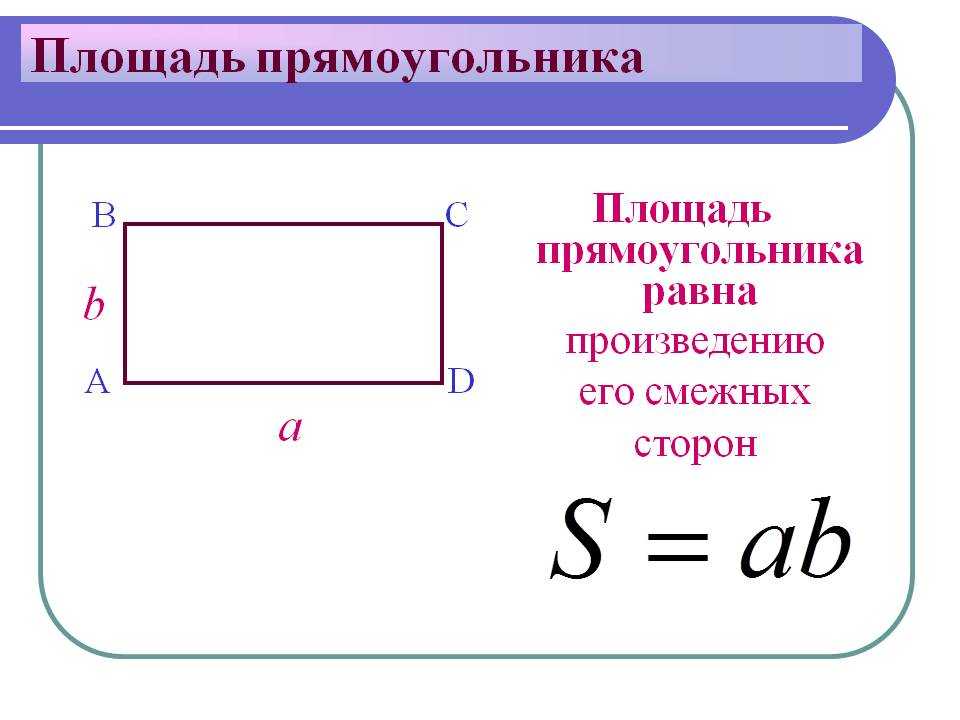
Формулы площади прямоугольника:

S = a · b.

Формула радиуса окружности, описанной вокруг прямоугольника:

Примечание: Фото https://www.pexels.com, https://pixabay.com

Найти что-нибудь еще?

карта сайта

Коэффициент востребованности
2 716

Свойства прямоугольника:

1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник

AB || CD, BC || AD

2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник

AB = CD, BC = AD

3. Стороны прямоугольника являются его высотами.

4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник

AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB

5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник

AC = BD

7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.

Рис. 7. Прямоугольник

△ABD = △BCD, △ABC = △ACD

8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).

Рис. 8. Прямоугольник

AC2 = AD2+ CD2

9. Диагонали прямоугольника делятся точкой пересечения пополам.

Рис. 9. Прямоугольник

AO = BO = CO = DO = АС2 = BD / 2

10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

Рис. 10. Прямоугольник

АС и BD – диаметр описанной окружности и диагональ прямоугольника

11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.

12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.

Рис. 11. Квадрат

AВ = ВC = AD = CD

Угол между диагоналями прямоугольника.

Формулы для определения угла меж диагоналей прямоугольника:

1. Формула определения угла меж диагоналей прямоугольника через угол между стороной и диагональю:

β = 2α

2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ.

При решении задач по школьной математике часто требуется определить, чему равняется диагональ заданного квадрата. При кажущейся некоторой сложности, эта задача является весьма простой и имеет несколько несложных способов решения. Рассмотрим их, для начала введём некоторые понятия и определения.

Квадрат
— это четырёхугольник с равными сторонами, все углы которого являются прямыми, то есть равны 90 градусов. Данная фигура одновременно и ромб, и прямоугольник, поэтому сохраняет все их свойства.
Диагональ многоугольника
— это отрезок, соединяющий две его противоположные вершины. В статье её будем обозначать буквой d.
Противоположными
называются вершины, не лежащие на одной стороне.
Корень квадратный из числа
, это такое число, которое при умножении само на себя даст исходное. В геометрии используются только положительные значения квадратного корня. В статье его будем обозначать сокращением rad (от латинского radical — корень).
Сторону квадрата будем обозначать буквой a.

Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.

Прямоугольник (понятие, определение):

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник – это четырехугольник, у которого каждый угол является прямым.

Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник

В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.

@ https://www.youtube.com/watch?v=_EVDcbOydAI

Решение примеров

Несмотря на то что формулы довольно простые, запомнить их простой зубрёжкой сложно. Чтобы материал закрепился, нужно научиться их применять на практике. Если понять принцип нахождения длины, многие из этих выражений можно будет вывести самостоятельно.

Вот некоторые задачи, рассчитанные на учащихся седьмых классов, рекомендуемые к самостоятельной проработке:

Определить длину прямоугольного многоугольника, у которого длина в 4 раза больше ширины. Периметр тела равен 20 см. Для решения задачи нужно принять сторону фигуры за х. Тогда длина будет составлять 4х. Согласно формуле, периметр равен: P = 2AB + 2 BC = 2* x + 2 * 4x. После подстановки значения P и выражения неизвестного, должно получиться следующее равенство: x = 20 / 10 = 2. Отсюда следует, что искомая длина равняется: BC = 4 * x = 4 * 2 = 8 см. Задача решена.
Длина прямоугольной фигуры больше её ширины на 2. Если ширина увеличится на 3 см, а длина на 8, площадь фигуры возрастёт в 3 раза. Найти длину. Чтобы решить задачу, нужно рассуждать следующим образом: пусть x ширина для первого состояния фигуры. Значит, длина этой фигуры будет x + 2. Соответственно, площадь равна: S = x * (x + 2). После трансформации ширина изменилась до значения x + 3, а длина — х + 2 + 8 = х + 10. Площадь новой фигуры равна: S = (х + 3) * (х + 10). После раскрытия скобок получится уравнение: 2 * х2 — 7* х — 30 = 0. После его решения должно получиться, что x = 6 см. Отсюда длина будет равняться: 6 + 2 = 8 см.
Определить длину и ширину прямоугольника ABCD, в который вписаны 3 круга, если радиус каждой описанной окружности равен 5 см. Для решения примера нужно вспомнить, что ширина многоугольника равна двум радиусам круга или его диаметру. Значит, AB = 2 * 5 = 10 см. Соответственно, длина будет составлять 3 диаметра или 6 радиусов: BC = 6 * 5 = 30 см. Ответ найден.

В процессе изучения материала совсем не зазорно пользоваться так называемыми онлайн-калькуляторами. Это сайты, предлагающие своим пользователям рассчитать различные математические величины по исходным данным. Их интересность не только в том, что можно получить готовый ответ, но и в появлении возможности просмотреть подробное решение. Это как раз и позволит устранить пробелы в знании на стадии обучения.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

Кроме этого:

1. Стороны прямоугольника являются его высотами.
2. Все углы прямоугольника прямые.
3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
4. Диагонали прямоугольника равны.
5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Задачи для самостоятельной работы:

1. Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

3. Рулон обоев имеет площадь 5 м2. Сколько нужно рулонов обоев, чтобы оклеить стену длиной 7 метров и высотой 3 метра?

Уважаемые читатели!

Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.

Материалы в архиве не помечены водяными знаками!

Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.

Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо!!!

Формулы нахождения длины

Существует несколько способов, позволяющих найти длину. Как лучше это сделать и какой алгоритм использовать, зависит от известных данных и личных предпочтений решающего. Как показывает практика, найти величину достаточно просто, если есть значение ширины и ещё одного из параметров многоугольника.

Найти длину (BC) прямоугольника можно следующим образом:

Зная площадь и ширину. Так как первая величина находится из произведения сторон S = AB * BC, длина будет равняться отношению размера замкнутой плоскости к ширине: BC = S/AB.
По известному периметру и примыкающей стороне. Периметр прямоугольника равен сумме всех его граней: P = AB + BC + CD + AD. Так как противолежащие стороны равны, равенство можно переписать так: P = 2AB + 2BC. Отсюда следует, что BC = (P — 2AB)/2.
Если известна диагональ и ширина. Отрезок, соединяющий противолежащие вершины, делит многоугольник на 2 прямоугольных треугольника, поэтому можно воспользоваться теоремой Пифагора: a = √ (‎ b2 + c2), где: a — гипотенуза (диагональ); b, с — катеты (ширина и длина). Отсюда: b = √ (c2 — a2) = ВС = √ CA2 — AB 2.
Используя формулу радиуса описанной окружности: R = √ (AB2 — BC2)/2. Для квадрата или ромба формула выглядит проще: R = a / √2 = d / 2, где d — диаметр описанного круга.

Диагональ прямоугольника можно вычислить через радиус описанной окружности d = 2 R или используя синус угла: d = a / sin (a), то есть найти из отношения прилегающей функции к ширине. Исходя из этого, можно вывести ещё одну формулу для поиска длины: BC = CA * cos (a).

Площадь фигуры можно найти не только как произведение сторон, но и зная размер диагонали с величиной синуса острого угла: S = d2 * sin (b) / 2, где b — угол между диагоналями. Приведённых формул будет достаточно для нахождения длины прямоугольника

При этом следует отметить важное свойство фигуры — высота многоугольника является шириной. Это свойство необходимо знать, так как в примерах нередко даётся размер не стороны, а именно высоты.

Как найти периметр прямоугольника?

Ниже в статье вы узнаете что такое и как найти периметр прямоугольника если известны его стороны. А также как найти стороны прямоугольника, если известен его периметр. И ещё одна интересная строительная прикладная задача.

Немного теории:

Периметр — это длина геометрической фигуры по её внешней границе.

Периметр прямоугольника — это сумма длин его сторон.

Формулы для вычисления периметра прямоугольника: P = 2*(a+b) или P = a + a + b + b.

Резюмируем! Для того чтобы вычислить периметр прямоугольника необходимо сложить все его стороны.

Типовые математические и практические задачи:

Исходные данные: Определить периметр прямоугольника с длинами сторон 5 см и 10 см.

Согласно формуле периметр прямоугольника равен = 2 * (5 + 10) = 30 см.

Исходные данные: Определить стороны прямоугольника выраженные целыми числами, если периметр прямоугольника равен 10.

По формуле определяем сумму длин сторон (a + b) = P / 2 = 10 / 2 = 5 Целыми значениями сторон могут быть только значения 1 + 4 = 5 и 2 + 3 = 5

Ответ: Длины сторон могут быть только 2 и 3 или 1 и 4.

Задача №3 (практическая):

Исходные данные: Определить число плинтусов в достаточном количестве для ремонта пола в комнате длиной 5 метров и шириной 3 метра, если длина одного плинтуса равна 3 метра.

Периметр комнаты = 2 * (5 + 3 ) = 16 метров Количество плинтусов = 16 / 3 = 5,33 штук Обычно в строительных магазинах плинтусы продаются не погонными метрами, а поштучно. Поэтому принимаем следующее целое число. Это шесть.

Ответ: Количество плинтусов 6 штук.

В заключение:

Решение задачи вычисления периметра является достаточно простой математической задачей, но имеющей очень важное практическое значение например в строительстве или генеральном планировании территории. На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника

С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина

На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника. С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина.

А о какой фигуре идет речь? Наверное, прямоугольник? Тогда надо перебрать все варианты. Ответов много. Если квадрат, то все проще. Из этого числа извлекаем квадратный корень. И это будет и ширина и длинна одновременно.

Если прямоугольник, то смотрим, на какие множители раскладывается это число ( площадь). И все они могут быть ответом. А с дробными числами их и вовсе огромное количество. Мало начальных данных для получения однозначного ответа.

Спасибо
Не нравится

Если речь идет о квадрате, то очень просто и однозначно. Нужно извлечь квадратный корень из площади, получим длину квадрата. У квадрата все стороны равны. В прямоугольнике длина далеко не всегда равна ширине. Если равна, то это уже частный случай — квадрат.

Рассмотрим случай, когда длина прямоугольника не равна ширине. Тогда узнать конкретную длину и ширину, зная только площадь, нельзя, т.к. вариантов будет много. Но если знать еще и соотношение сторон прямоугольника, то вычисление однозначного ответа становится возможным.

Например, есть прямоугольник площадью 100 квадратных единиц, а соотношение сторон неизвестно. Значит, стороны могут быть равными 1 и 100 единиц, 2 и 50, и и 25 и так далее. И никто не отменят варианты с дробными длинами.

Когда соотношение сторон дано, то можно точно вычислить и сами стороны.

Например, площадь прямоугольника равна 100 квадратных единиц, соотношение сторон 1:4.

Тогда по формуле площади можно составить уравнение и найти стороны.

x = 5. Второй корень уравнения — минус 5 — не подходит, т.к. длина не может быть отрицательной.