Нахождение сторон прямоугольника при известных периметре и площади
Рассмотрим первую задачу:
Как известно, периметр прямоугольника находится по формуле \({\color{red} P=2\cdot (a+b)}\) , площадь – по формуле \({\color{red} S=a\cdot b}\) .
Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:
\({\color{red} a + b = 24 : 2 = 12}\) см.
А дальше мы рассуждаем так.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной \({\color{red} 12 : 2 = 6}\) см.
Тогда площадь этого квадрата равна
\({\color{red}S_{k}=6\cdot 6=36}\) см2.
По условию нашей задачи площадь прямоугольника составляет 32 см2. Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.
\({\color{red} S–S _{k}=36-32=4}\) см2.
Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.
Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной. То есть, ширину уменьшить, а длину увеличить на одно и то же число.
Но на какое?
Площадь 4 см2 – это квадрат со стороной 2 см. Это и есть нужное нам число.
Тогда, ширина искомого прямоугольника будет равна:
\({\color{red} a=6-2=4}\) см
а длина:
\({\color{red} b=6+2=8}\) см.
Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:
\({\color{red} P=2\cdot (4+8)=2\cdot 12=24}\) см
\({\color{red} S=4\cdot 8=32}\) см2.
Задача решена верно.
Теперь рассмотрим вторую задачу.
Находим полупериметр, то есть, сумму двух сторон прямоугольника.
\({\color{red} a+b=46:2=23}\) см.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица. Это прямоугольник со сторонами 11 и 12, т.к. \({\color{red} 23=11+12}\).
Площадь такого прямоугольника равна:
\({\color{red}S_{2}=11\cdot 12=132}\) см2.
Разница между полученной площадью и заданной по условию задачи составляет:
\({\color{red}S_{2}-S=132-126=6}\) см2.
6 см2 – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.
Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см2, а именно, на 2.
Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).
Находим ширину искомого прямоугольника:
\({\color{red} a=11-2=9}\) см.
Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:
\({\color{red} b=12+2=14}\) см.
Проведем проверку:
\({\color{red} P=2\cdot (9+14)=2\cdot 23=46}\) см.
\({\color{red}S=9\cdot 14=126}\) см2.
И эта задача решена тоже верно.
На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.
Вам также пригодится:
Текстовые задачи в начальной школе – так ли трудно научиться их решать?
Как научить ребенка преодолевать трудности?
6 правил, которые научат ребенка собранности
Решение вирусных школьных задач
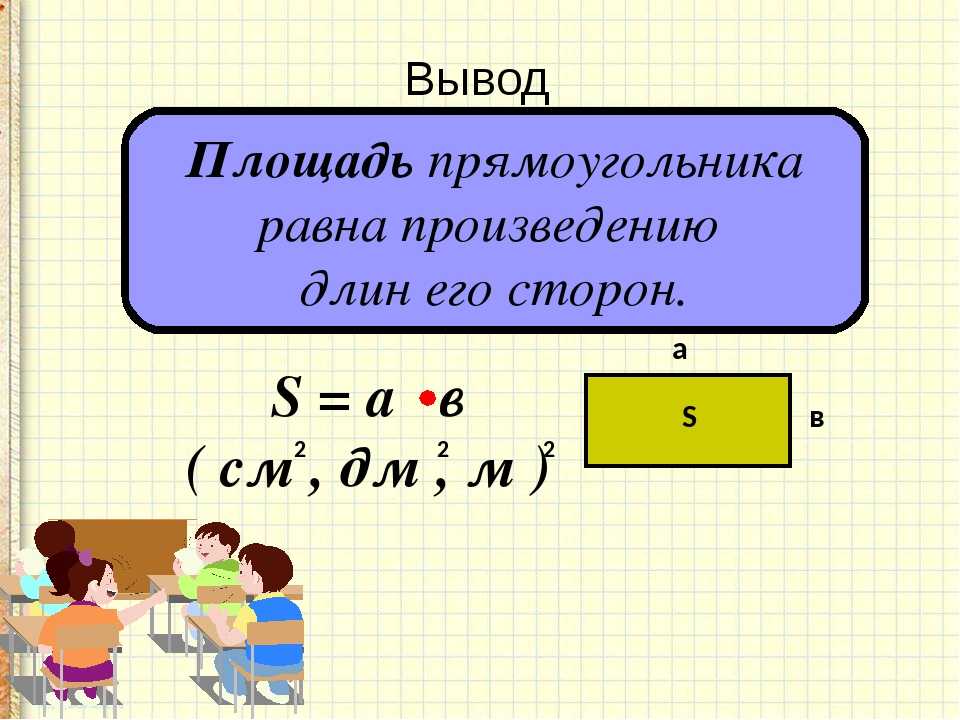
Формула площади прямоугольника
Площадь прямоугольника равна произведению его ширины на высоту.
S=a*b.
Если задано длину диагоналей (d) и угол между ними (alpha) то формула площади прямоугольника равна половине квадрата диагоналей на синус угла между ними.
S=d*d*sin(alpha)/2.
Не забывайте что площадь измеряется в единицах квадратных, поэтому если размеры заданы в метрах то площадь будет в метрах квадратных, сантиметрах — площадь в сантиметрах квадратных и т.п.
Пример 2. Диагонали прямоугольника пересекаются под углом 30 градусов и ровны 5 см. Какова площадь прямоугольника?
Решение. Подставляем данные в формулу площади прямоугольника через диагонали
Ответ. Площадь равна 6,25 сантиметров квадратных.
Диагонали прямоугольника
В прямоугольнике длину диагонали вычисляют через длины сторон по теореме Пифагора
d=sqrt(a^2+b^2) или
Итак Вы уже знаете как найти площадь прямоугольника, периметр и диагональ.
Если известна диагональ и одна сторона то вторую также определяем по теореме Пифагора
или
Описанная и вписанная окружность в прямоугольник
Диаметр или радиус описанной вокруг прямоугольника окружности Вы видимо вычисляли. Однако вряд ли задумывались о вписанной окружности и геометрическом место ее центров.
![]()
Диаметр описанной окружности равен диагонали (d), соответственно радиус описанной окружности — половине диагонали (R=d/2). Вписанных окружностей в прямоугольник можно построить множество. Радиус вписанной окружности равен половине длины меньшей стороны прямоугольника (r=b/2). Если соединить центры всех возможных вписанных окружностей то получим отрезок MN длина которого равна разности сторон (MN=a-b).
Приведенная информация о вписанной и описанной окружности редко пригодится Вам при решении задач но Вы должны знать как в таких случаях вычислять указанные величины.
Задачи для самостоятельной работы:
1. Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
3. Рулон обоев имеет площадь 5 м2. Сколько нужно рулонов обоев, чтобы оклеить стену длиной 7 метров и высотой 3 метра?
Уважаемые читатели!
Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.
Материалы в архиве не помечены водяными знаками!
Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.
Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо!!!
Способы нахождения
По трем сторонам
Если мы уже знаем длину каждого ребра фигуры, расчет периметра будет проходить так:
\(P = a+b+c\)
где a, b и с — это стороны треугольника.
В случае, если нам известны стороны равнобедренного треугольника (у которого два ребра равны), формула для расчета периметра выглядит следующим образом:
\(P=a+2b\) или \(P=a+2c \)
где a — основание фигуры, а b и с — равные ребра.
Треугольник может также быть равносторонним (когда все стороны равны). Тогда P будем находить в соответствии с расчетами:
\(P=3a\)
где a — это любая сторона фигуры.
По площади и радиусу вписанной окружности
Когда нам известна площадь данного многоугольника и радиус вписанной в него окружности, расчет P выглядит так:
\(P=\frac{2S}r\)
где S — площадь фигуры, r — радиус вписанной в нее окружности.
По двум сторонам и углу между ними
Так как нам известен угол и две стороны, которыми он образован, мы можем найти третью сторону треугольника по теореме косинусов. И потом уже вычислить сумму длин всех ребер фигуры.
Теорема косинусов выглядит так:
\(a^2=b^2+c^2-2bc\times\cos\alpha\)
где α — известный угол.
Тогда формула для расчета периметра всей фигуры в этом случае:
\(P=\sqrt{b^2+c^2-2bc\times\cos\alpha}+b+c\)
По боковой стороне и высоте (для равнобедренного)
Возвращаясь к свойствам равнобедренного треугольника, вспоминаем, что высота, проведенная к основанию треугольника из противоположной вершины, является одновременно высотой, биссектрисой и медианой. Это значит, что оба прямоугольных треугольника, которые она образует, равны между собой.
Формула для поиска периметра нашего равнобедренного будет опираться на теорему Пифагора. Пусть 1/2 основания (с) = d. Тогда:
\(d^2=a^2-h^2\)
\(d=\sqrt{a^2-h^2}\)
где a — сторона равнобедренного треугольника и гипотенуза прямоугольного, h — высота равнобедренного и катет прямоугольного.
Не забываем, что d — это лишь половина основания равнобедренного треугольника, поэтому для поиска периметра результат нужно будет умножить на 2.
\(P=2\sqrt{a^2-h^2}+2a\)
По двум катетам (для прямоугольного)
Еще раз вспомним теорему Пифагора для нахождения гипотенузы (обозначим ее буквой с).
\(c^2=a^2+b^2\)
\(c=\sqrt{a^2+b^2}\)
где a и b — катеты треугольника.
Подставляем значение c в формулу для нахождения периметра и получаем:
\(P=\sqrt{a^2+b^2}+a+b\)
Правило встречается в следующих упражнениях:
1 класс
Страница 4. Урок 3,
Петерсон, Учебник, часть 3
Страница 5. Урок 3,
Петерсон, Учебник, часть 3
Страница 87. Урок 44,
Петерсон, Учебник, часть 3
2 класс
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 65,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 64. Вариант 1. Тест 1,
Моро, Волкова, Проверочные работы
Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 43. Урок 22,
Петерсон, Учебник, часть 1
3 класс
Страница 78,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 14. Вариант 1. № 2,
Моро, Волкова, Проверочные работы
Страница 44. Вариант 1. Тест 2,
Моро, Волкова, Проверочные работы
Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 79,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 70,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 103,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 65,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 207,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 208,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 209,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 210,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
6 класс
Задание 389,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 428,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 430,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Ход урока
I. Организационный момент.
— Добрый день! Наша основная задачана сегодняшнем уроке: ду-мать, смекать и считать. А ещё мы попробуем разобраться с тем, как с помощью математики сказку сделать былью.
— Кто из вас любит читать сказки?
— А какие сказки мы называем волшебными?
II. Актуализация опорных знаний.
— Для начала расшифруем фразу, которая спряталась в примерах.
36 8 27 54 9 8 5 72 7 63 7 81 6 63 1
(Получится фраза «О чём мечтали люди)
3 см * 9 = … см (е)8 дм 1 см : 9 = … см (е) 9 см * 4 = … см (о) 7 дм * 9 = …дм (и) 9 дм * 9 = … дм (ю)7 дм 2 см : 9 = … см (ч)6 дм 3 см : 9 = … см (л)5 дм 4 см : 9 = … см (д)4 дм 5 см : 9 = … см (т)9 дм : 9 = … дм) 9 см * 8 = … см (а) 9 * 6 дм = … дм (м)
— Народ слагал сказки тысячи лет назад, когда ещё не умел читать и писать. В своих сказках люди выражали свои мечты и надежды. Им очень хотелось иметь ковёр-самолёт, чтобы быстрее передвигаться. И вот менее 100 лет назад люди, хорошо знающие математику и законы физики, изобрели… (самолёт)
— Люди мечтали о ярком свете ночью, и что же они придумали в помощь сказочным героям? (Перо жар-птицы) Какой предмет теперь освещает пространство в ночное время? (Прожектор, электрические све-тильники)
— Подумайте и скажите, какие предметы люди придумали в сказках, чтобы быстрее передвигаться, находить дорогу в незнакомой местности, иметь возможность пообедать в дороге. Назовите реальные предметы и сказочные аналоги.
(Скатерть-самобранка – кафе или рестораны; ковёр-самолёт – само-лёт;; чудо-зеркальце – телевизор; сани-самокаты – аэросани; конёк гор-бунок – космическая ракета; клубок ниток, указывающий путь – компас и карта; сапоги-скороходы – машины; золотой петушок – радиолока-тор)
III. Постановка темы урока.
— Какой предмет Василиса Прекрасная должна была выткать за од-ну ночь? (Ковёр)
— Не просто ковёр, а ковёр по заданным размера – периметр равен числу, состоящему из четырёх четвёрок метров. Это сколько? (16 мет-ров)
— Только вот я разволновалась и забыла, что такое периметр. Вы поможете мне на уроке разобраться в этом?
— Давайте вспомним, что мы называем периметром?
(Дети вспоминают формулы нахождения периметра прямоуголь-ника и квадрата.)
— Давайте потренируемся находить периметр квадрата.
Возьми линейку, карандаш
И начерти квадрат.
Да повнимательней следи,
Чтоб не был кривоват.
Отметим в стороны:
5 сантиметров пусть.
(Дети вычерчивают длину)
Теперь задание, и ты
Внимательнее будь.
Ты сумму всех его сторон,
Пожалуйста, найди.
И самый быстрый способ ты
В ответе приведи.
(Дети самостоятельно находят периметр.)
— Сегодня на уроке нам предстоит расширить наши знания о квад-рате. Попробуем найти периметр волшебного платочка со сторонами 9 дм и 7 дм. Что это за фигура? Какая геометрическая фигура называется прямоугольником?
— Как мы можем найти периметр прямоугольника?
Р = a + b + c + d
P = (a + b) * 2
P = a * 2 + b * 2
— Возьмите в руки белые прямоугольники, которые лежат у вас на парте, измерьте их стороны и найдите периметр. Решение запишите в тетрадь. Чему равен периметр этих прямоугольников?
— А что вот это за фигура? (Показываю квадрат.)
— Как доказать, что это квадрат? (У квадрата все углы прямые и все стороны равны между собой)
— Начертите в тетрадях квадрат со стороной 6 см. Найдите его пе-риметр.
— Как удобнее найти периметр квадрата?
— А можем ли мы у прямоугольника, который не является квадра-том, так же найти периметр? Почему?
— Возьмите лежащие у вас на парте квадраты, измерьте их стороны и найдите периметр. Запишите решение в тетрадь.
— А теперь займёмся повторением и закреплением изученного.
1. Сколько дециметров в 1 м? Решите примеры.
6 дм 6 см = … см 4 дм 30 см = … дм … см
4 дм 3 см = … см 3 дм 55 см = … дм … см
2. Найдите состав именованного числа
38 см = … дм … см 79 см = … дм … см
100 см = … дм 5 дм = … см
IV. Формирование вычислительных навыков.
1. Математические загадки.
а) Игорь начертил 2 отрезка. Второй отрезок у него получился на 40 см длиннее первого. А его длина – 2 см. Какова длина первого отрез-ка?
б) Таня тоже начертила 2 отрезка. Второй отрезок у неё получился короче первого на 1 дм, а длина второго отрезка – 5 дм.
в) Борис начертил квадрат со стороной 5 дм. Какой у квадрата пе-риметр?
г) Саша измерил длину и ширину своего стола. Оказалось, что длина равна 1 м, а ширина – 6 дм 7 см. На сколько длина стола больше его ширины?
д) От куска ленты отрезали сначала 6 дм 2 см, а потом ещё 1 дм 3 см. Сколько всего отрезали ленты.
2. Далее учитель работал по учебнику.
V. Итоги урока.
— Какие правила и понятия по математике мы сегодня вспом-нили?
— У кого из вас действия с измерением длины и вычисления с единицами её измерения вызывает затруднения?
VI. Домашнее задание.
— Выбрать любые сказки и в связи с ними составить задачи, связан-ные с длиной, расстоянием, вычислением периметра. И решить их.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
Кроме этого:
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Шаги
Метод 1 из 6: Прямоугольник
-
1
Найдите длины двух смежных сторон:Если даны только одна сторона и площадь прямоугольника, вы можете найти другую сторону по формуле: A=wh, то есть h=A/w или w=A/h. Поэтому, если даны высота и площадь, просто разделите площадь на высоту, чтобы найти ширину. Вы также можете разделить площадь на ширину, чтобы найти высоту.
ширины и высоты. Прямоугольник – фигура с четырьмя сторонами, которые пересекаются под прямым углом, а две противоположные стороны параллельны и равны. Таким образом, две смежные стороны имеют разную длину (ширина и высота; если ширина равна высоте, то такая фигура – квадрат).
-
2
Сложите длины двух смежных сторон и умножьте полученное значение на 2. Если w — ширина и h — высота, периметр прямоугольника: P=2(w+h)
Метод 2 из 6: Квадрат
-
1
Найдите длину стороны квадрата (назовем ее х). Квадрат – фигура, у которой все стороны равны и пресекаются под прямым углом. -
2
Если дана площадь (A) квадрата, вы можете найти длину стороны, взяв квадратный корень из площади:Если дана диагональ (d) квадрата, Вы можете найти длину стороны, разделив диагональ на квадратный корень из 2: х = d/√2
х = √ (A).
-
3
Умножьте длину стороны на четыре. Поскольку все четыре стороны имеют одинаковую длину, периметр квадрата равен учетверенной длине одной стороны: Р = 4x.
Метод 3 из 6: Круг
-
1
Найдите длину радиуса (r). Радиус является расстоянием от центра круга до любой точки на окружности.- Если дан диаметр (d) круга, вы можете найти радиус, разделив диаметр на два: г = d/2
- Если дана площадь (A) круга, вы можете найти радиус, разделив площадь на π, а затем взяв квадратный корень из полученного значения: г = √(A/π)
-
2
Найдите периметр, умножив радиус на 2π:Так как диаметр — это удвоенный радиус, периметр может быть найден по формуле: P = πd.
Р = 2πr.
Метод 4 из 6: Прямоугольный треугольник
-
1
Найдите длины двух сторон треугольника (а и b), пересекающихся под прямым углом. -
2
Найдите сумму квадратов а и b, а затем извлеките квадратный корень из полученной суммы: √(а^2 + b^2). По теореме Пифагора, а^2 + b^2 = с^2, где с — длина гипотенузы, то есть стороны, лежащей напротив прямого угла. -
3
Теперь, когда у вас есть а, b и с (все три стороны треугольника), просто сложите их для нахождения периметра: P = а+b+с.
Метод 5 из 6: Треугольник
-
1
Найдите высоту треугольника (у) и его основание (х) (сторона, к которой проведен перпендикуляр – высота). -
2
Найдите длины отрезков х1 и х2, на которые высота делит основание (то есть х = х1 + х2). Высота делит треугольник на два прямоугольных треугольника (один с катетами х1 и у, другой с катетами х2 и у), и необходимо найти длины гипотенуз этих треугольников с1 и с2. -
3
Найдите с1 и с2. Для этого используйте теорему Пифагора: а^2 + b^2 = с^2, и подставьте x1 вместо a, y вместо b, c1 вместо c. Повторите для х2, у, и с2. -
4
Сложите х, с1 и с2, которые являются тремя сторонами исходного треугольника.
Метод 6 из 6: Правильный многоугольник
-
1
Найдите длину одной стороны правильного многоугольника. По определению, правильный многоугольник – это фигура с равными сторонами и углами.- Если дана апофема (перпендикуляр, опущенный из центра многоугольника к одной из его сторон), Вы можете найти длину стороны. Если n – число сторон многоугольника, А – длина апофемы, длина стороны: x=2Atan(180/n).
- Если дан радиус (расстояние между центром и любой вершиной), вы можете найти длину стороны: x=2rsin(180/n), где r – радиус, n – число сторон многоугольника.
-
2
Умножьте длину одной стороны многоугольника на число его сторон. Таким образом, P=nx, где n – число сторон многоугольника, х – длина одной стороны многоугольника.
Стандартный метод
В зависимости от сложности вычислений, применяют одну из формул, чтобы высчитать периметр. Учащиеся начальной школы знакомятся с понятием, сталкиваясь с практическими задачами.
Задача
Найти длину забора участка прямоугольной формы, который надо построить Сидору Карловичу, если общая граница с участком Ивана Петровича составляет 3 метра, а с плантацией Марии Ивановны – 5 метров.
Решение
Чтобы решить задачу и помочь незадачливому Сидору Карловичу, ученику приходится использовать формулу периметра прямоугольника. Учитывая, что a = 3, b = 5, дети легко находят, что длина забора равна
P = 2 (a + b) = 2 * (3 + 5) = 2 * 8 = 16 (метров)
Важные требования, предъявляемые к ученикам на данном этапе изучения материала, заключаются в правильном соизмерении длины и ширины, а также в умении начертить фигуру.
Работа выполняется только при одинаковых единицах измерения, все чертежи делаются строго с использованием инструментов!
Часто длина заданного отрезка измеряется непосредственно.
Формула площади прямоугольника
Площадь прямоугольника равна произведению его ширины на высоту.
S=a*b.
Если задано длину диагоналей (d) и угол между ними (alpha) то формула площади прямоугольника равна половине квадрата диагоналей на синус угла между ними.
S=d*d*sin(alpha)/2.
Не забывайте что площадь измеряется в единицах квадратных, поэтому если размеры заданы в метрах то площадь будет в метрах квадратных, сантиметрах – площадь в сантиметрах квадратных и т.п.
Пример 2. Диагонали прямоугольника пересекаются под углом 30 градусов и ровны 5 см. Какова площадь прямоугольника?
Решение. Подставляем данные в формулу площади прямоугольника через диагонали
Ответ. Площадь равна 6,25 сантиметров квадратных.
Диагонали прямоугольника
В прямоугольнике длину диагонали вычисляют через длины сторон по теореме Пифагора
d=sqrt(a^2+b^2) или
Итак Вы уже знаете как найти площадь прямоугольника, периметр и диагональ.
Задачи на прямоугольник
Стороны прямоугольника
Задача 1. Длина диагонали и стороны прямоугольника составляют 10 и 8 см. Найдите другую сторону.
Решение. По теореме Пифагора вычисляем
Ответ. Сторона равна 6 см.
——————————-
Задача 2. Длина диагонали прямоугольника равна 5 см. Одна сторона меньше другой на сантиметр. Найдите стороны прямоугольника.
Решение. Обозначим первую сторону через х, тогда по условию вторая – х -1. Составляем уравнение
Возводим к квадрату и решаем квадратное уравнение
Второе значение не имеет смысла. Для вычисления меньшей стороны выполняем вычитание
Ответ. Стороны прямоугольника равны 3 и 4 см.
——————————-
Задачи на площадь и периметр прямоугольника
Задача 3. Большая сторона прямоугольника 8 см. Меньшая составляет четверть большой. Какая площадь и периметр прямоугольника?
Решение. Четверть большей означает одна четвертая часть, то есть
b= 8/4=2 (см).
Площадь и периметр находим по формулам
P=2(2+8)=20 (см); S=2*8=16 (см^2).
Ответ. Периметр 20 см, площадь 16 сантиметров квадратных.
——————————-
Задача 4. Участок земли имеет площадь 64 квадратных метров. Какой периметр участка если диагонали пересекаются под прямым углом?
Решение.
Поскольку угол между диагоналями 90 градусов, то это квадрат. Площадь квадрата равна квадрату стороны Отсюда находим сторону Периметр находим по формуле
Ответ. Периметр равен 32 метра.
Не забывайте что периметр измеряется в единицах длины, а площадь — в единицах квадратных.
Теперь Вы знаете как найти периметр и площадь прямоугольника. Пользуйтесь формулами на практике и совершенствуйте навыки вычислений указанных величин.
Посмотреть материалы:
- Прямоугольный треугольник. Задачи
- Площадь треугольника. Формулы
- Квадрат. Формулы
- Периметр и площадь параллелограмма
- Формулы площади трапеции
- Ромб. Площадь, периметр
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.