Определения и соглашения
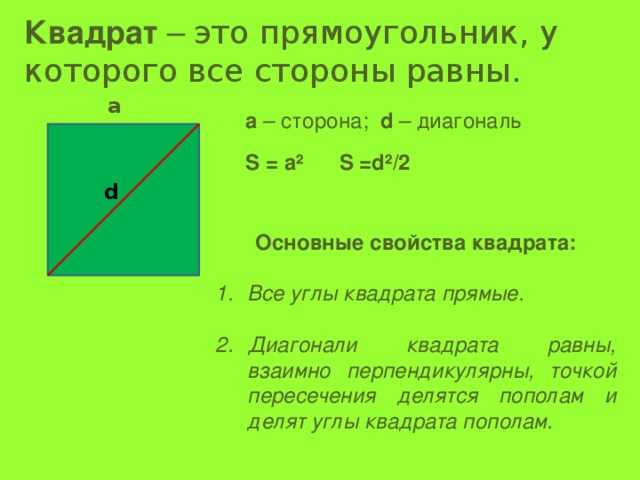
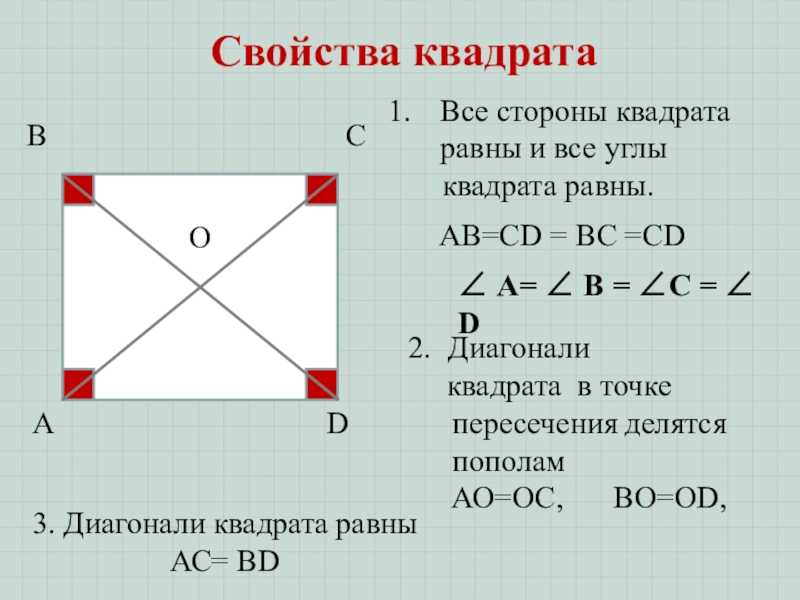
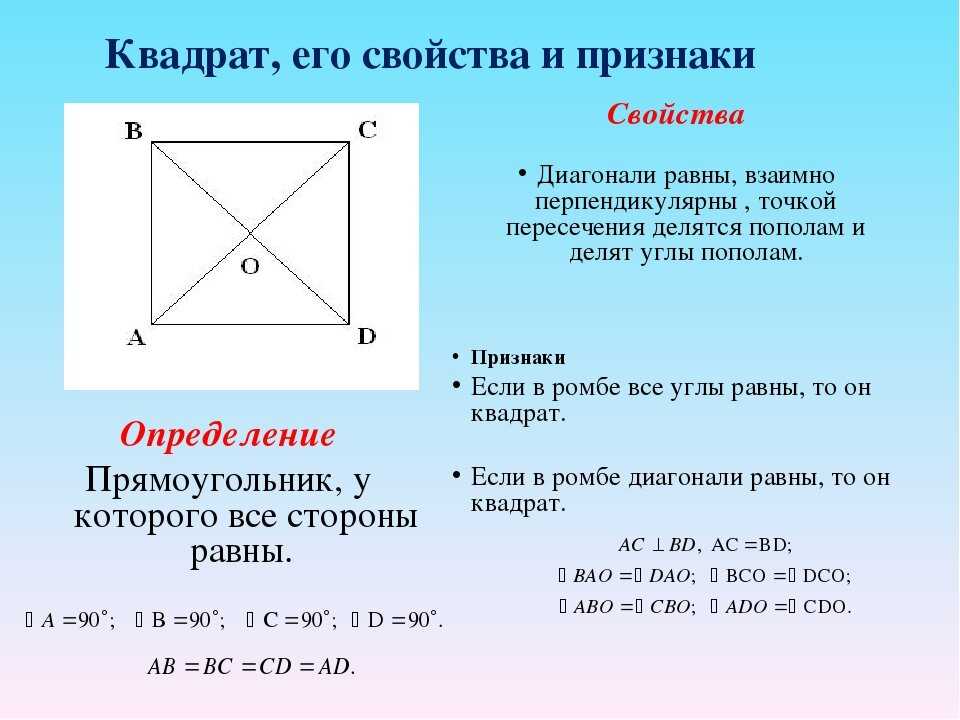
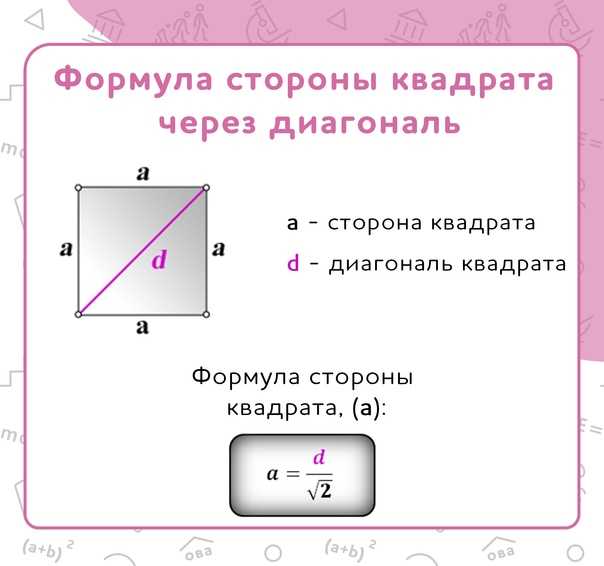
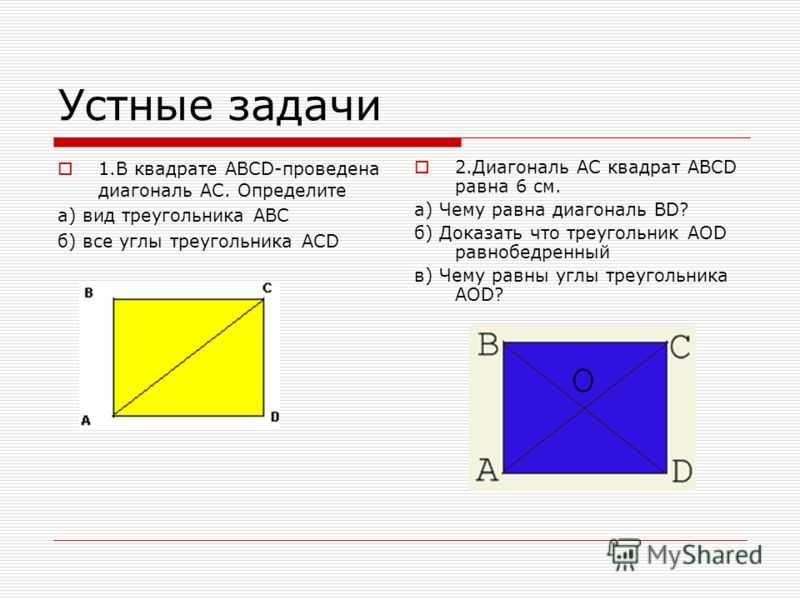
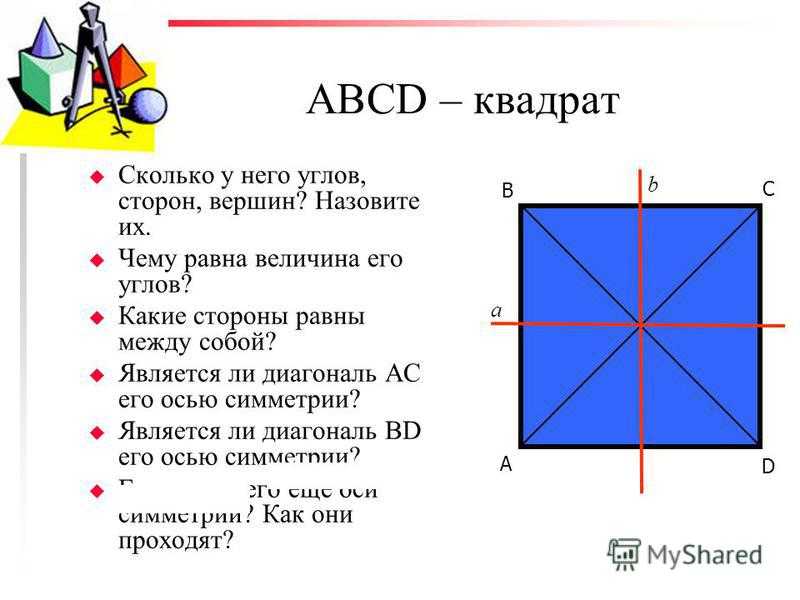
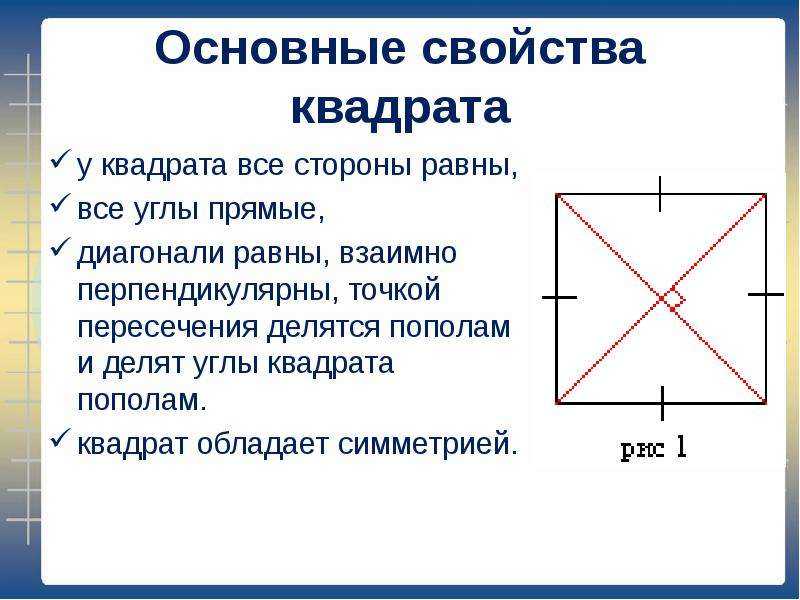
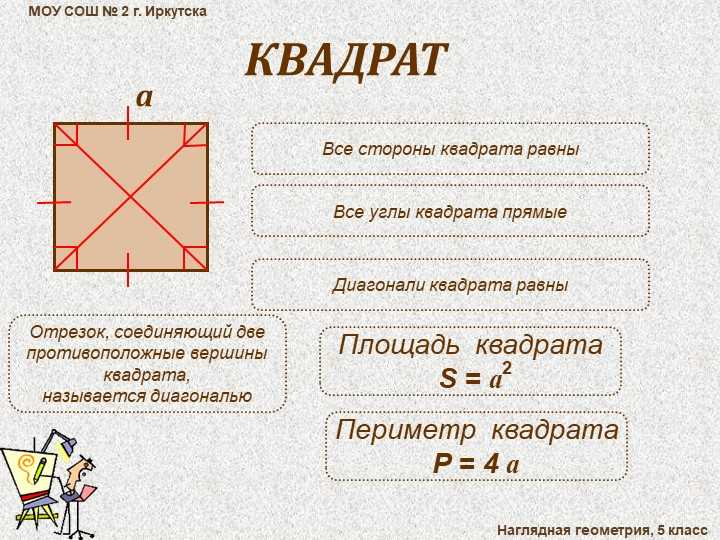
- Квадрат — это четырёхугольник с равными сторонами, все углы которого являются прямыми, то есть равны 90 градусов. Данная фигура одновременно и ромб, и прямоугольник, поэтому сохраняет все их свойства.
- Диагональ многоугольника — это отрезок, соединяющий две его противоположные вершины. В статье её будем обозначать буквой d.
- Противоположными называются вершины, не лежащие на одной стороне.
- Корень квадратный из числа, это такое число, которое при умножении само на себя даст исходное. В геометрии используются только положительные значения квадратного корня. В статье его будем обозначать сокращением rad (от латинского radical — корень).
- Сторону квадрата будем обозначать буквой a.
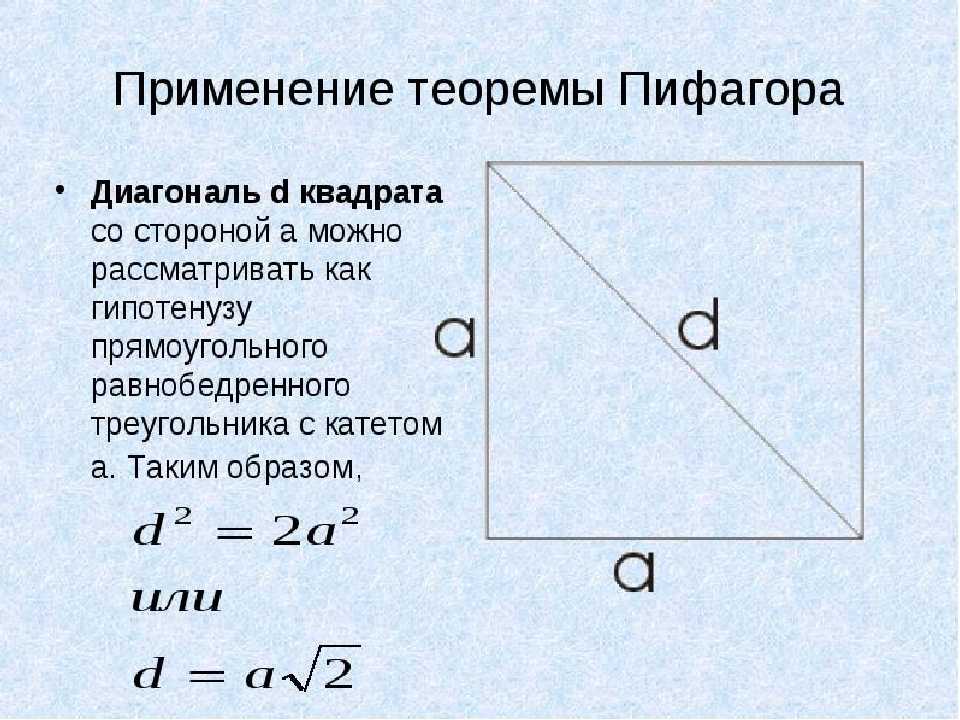
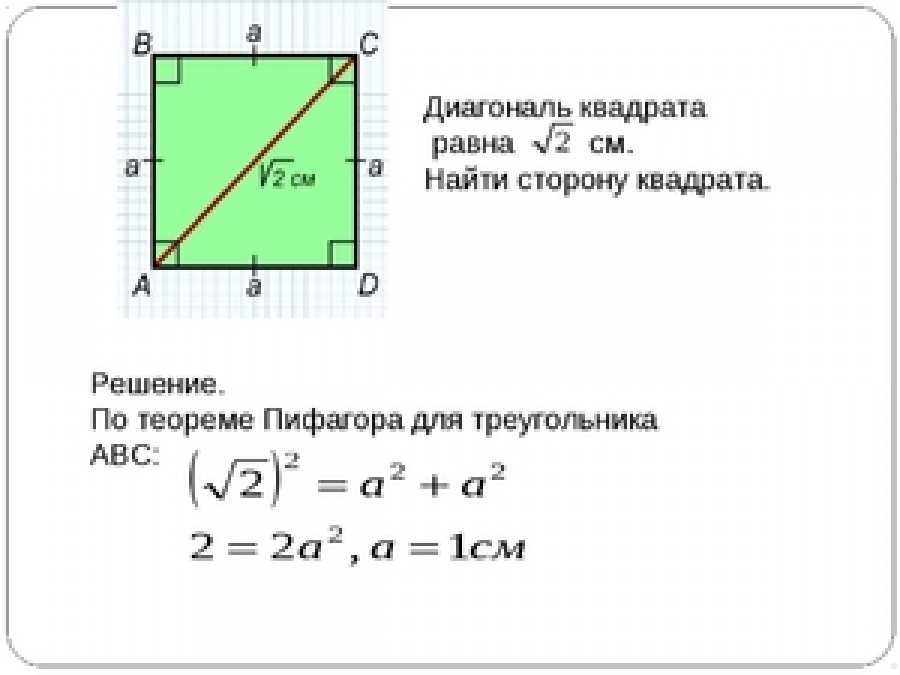
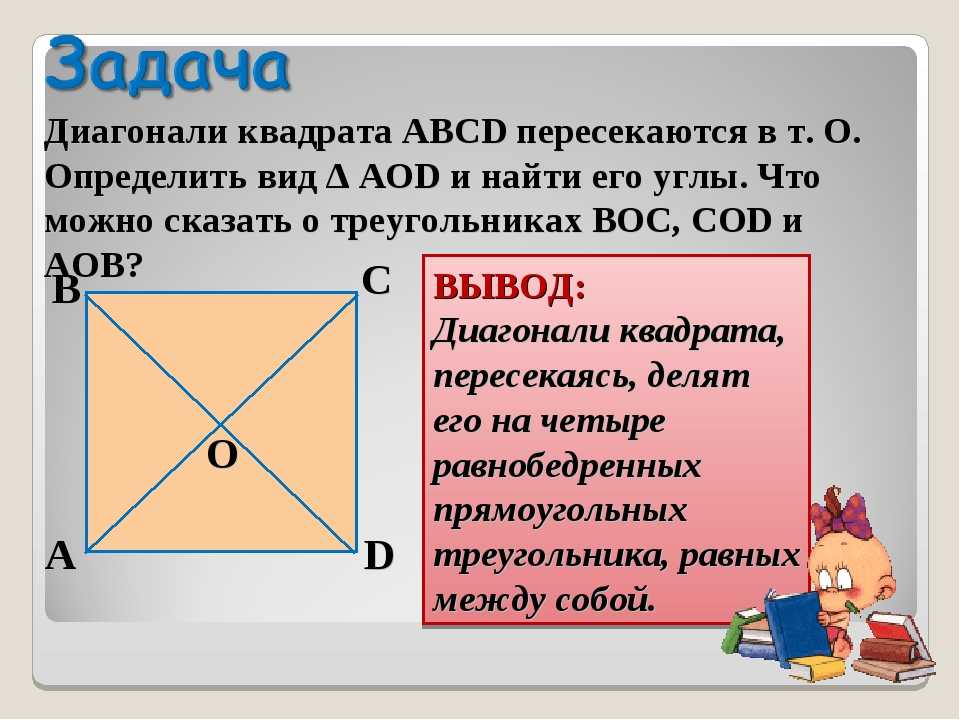
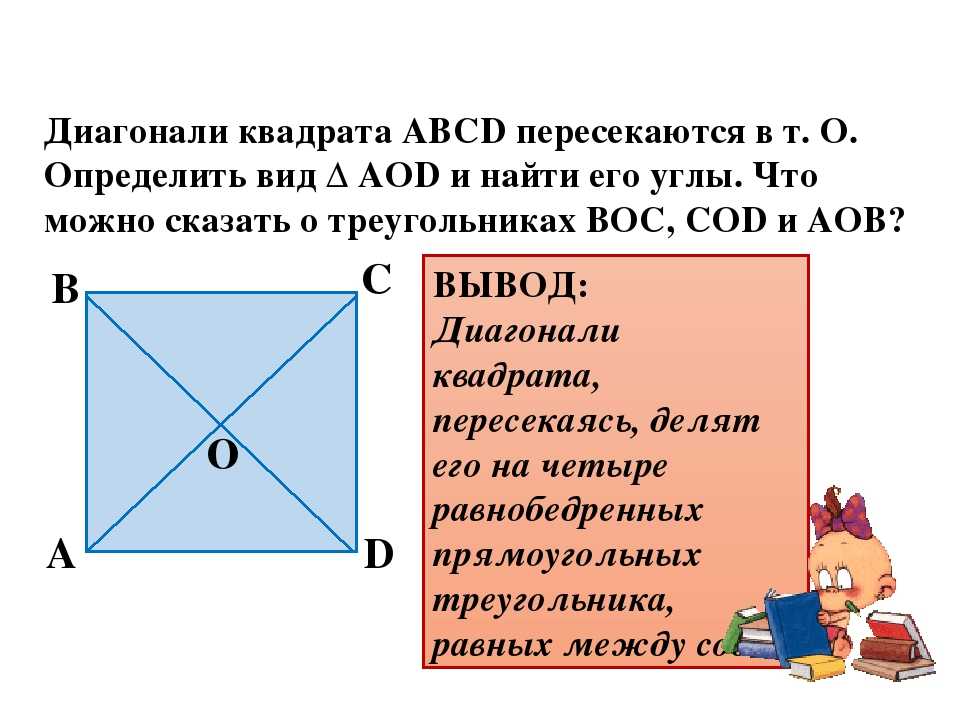
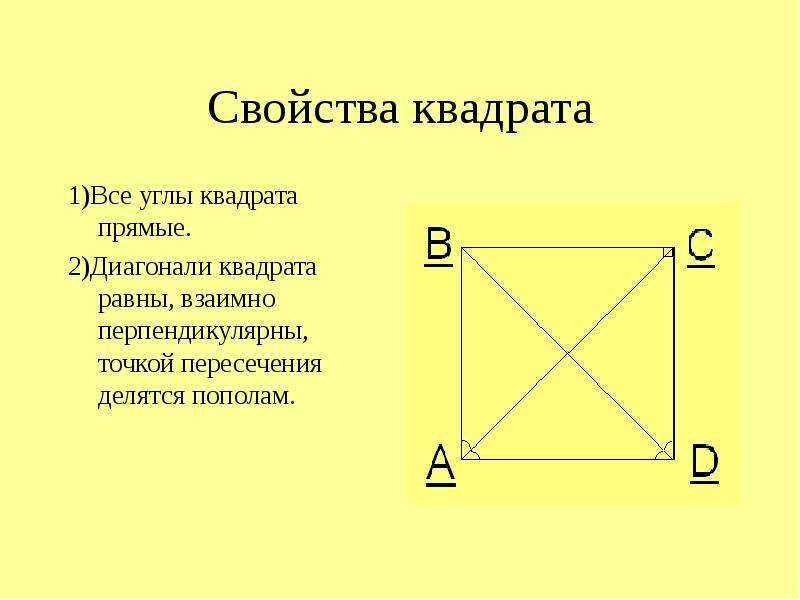
Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.
Вычисление по радиусу описанной и вписанной окружности
Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
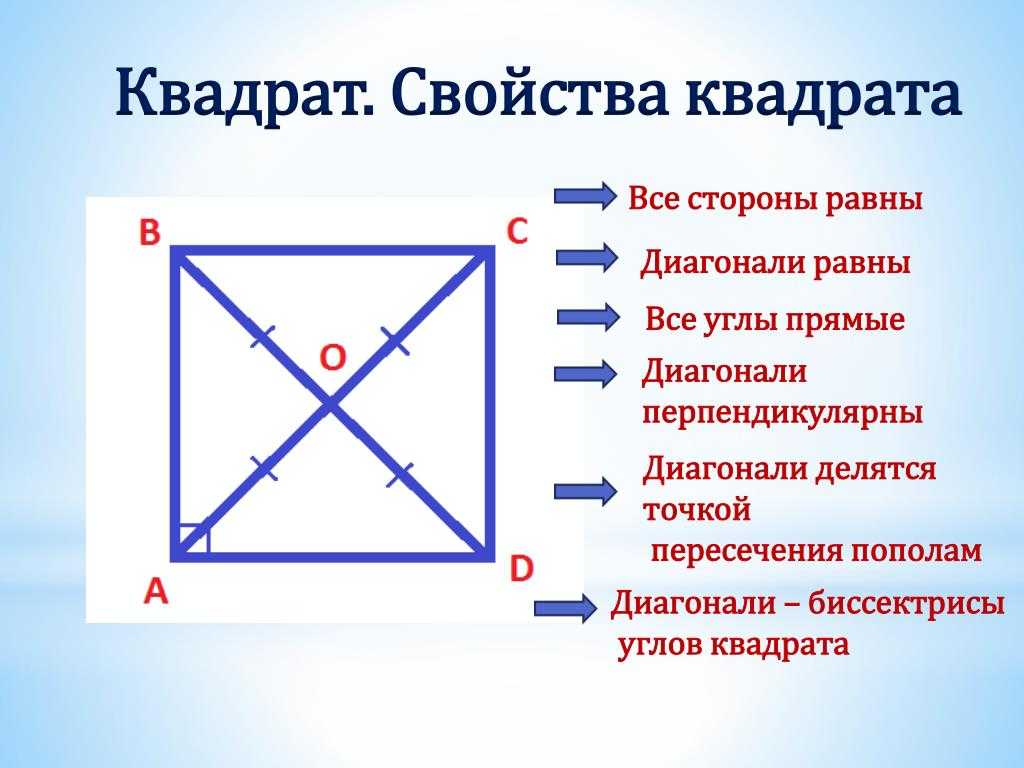
Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.
И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.
Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.
Чему равна диагональ квадрата? Как найти диагональ квадрата?
|
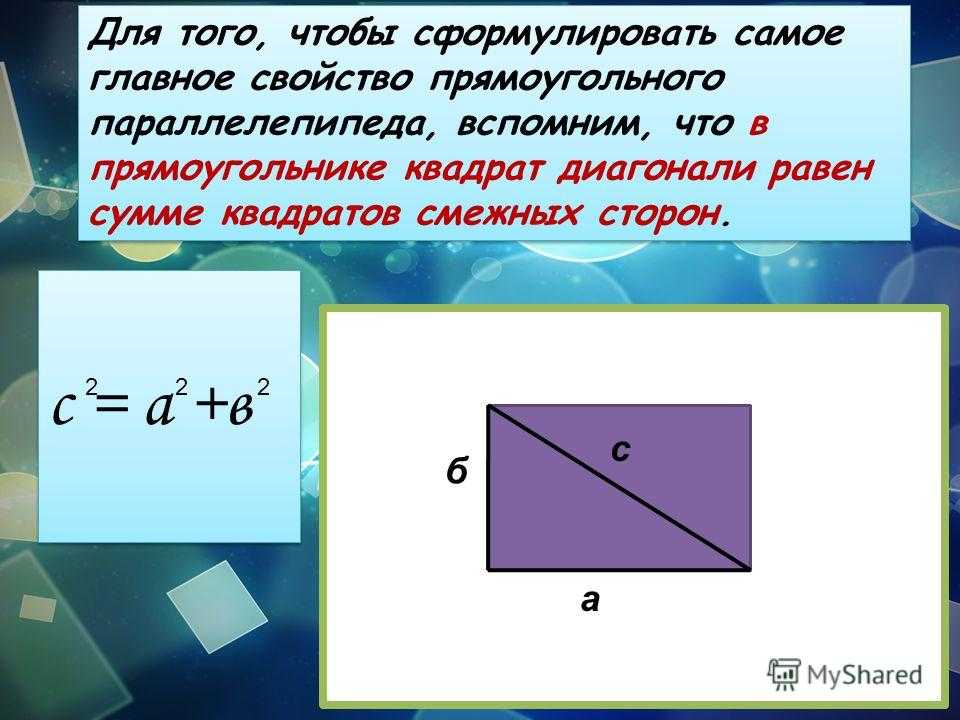
bezdelnik 7 лет назад Длину d диагонали квадрата по отношению к длине b его стороны находят по теореме Пифагора на основании того, что все стороны квадрата равны и все углы, образованные сторонами квадрата, прямые. Поэтому сумма квадратов двух сторон равна квадрату диагонали, являющейся гипотенузой прямоугольного треугольника: 2b^2=d^2, d= b√2. Если принять сторону квадрата за единицу, то d= √2=1,414… . автор вопроса выбрал этот ответ лучшим Степан-16 4 года назад Диагональ (с) — это гипотенуза треугольника, у которого катеты (а и а, поскольку они равны) — это две стороны квадрата. Два способа решения.
Алиса в Стране 4 года назад Если поделить квадрат диагональю, то мы увидим перед собой два одинаковых прямоугольных треугольника, а диагональ квадрата будет для любого из этих треугольников гипотенузой. А как рассчитывать длину гипотенузы, зная длину катетов, мы все знаем. Для этого у нас имеется теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Катеты у нас равны друг другу (потому что у нас квадрат), значит, обозначив длину катета латинской буквой «а», а длину гипотенузы латинской буквой «с», получаем формулу: c² = a² + a² = 2 a² с = √2a. Ответ: диагональ квадрата равна квадратному корню из суммы квадратов его сторон. Ксарфакс 4 года назад Диагональ квадрата представляет собой отрезок, соединяющий две противоположные вершины. В то же время диагональ разбивает квадрат на 2 равных прямоугольных треугольника. Таким образом, чтобы найти диагональ квадрата, следует воспользоваться теоремой Пифагора. a² + b² = c². Пусть c — это диагональ, a и b — стороны квадрата, которые по определению равны между собой. Перепишем формулу в виде: 2a² = c². Выразим диагональ c: c = √2 * a. Таким образом, диагональ квадрата равна произведению его стороны на квадратный корень из числа 2. Пример Сторона квадрата равна 10 см. Диагональ будет равна 10 * √2 см ≈ 14 см. terli4eno4ka 4 года назад Под диагональю квадрата понимается отрезок, соединяющий противоположные углы квадрата. Для того, чтобы найти диагональ квадрата, можно воспользоваться следующими формулами, для которых нужно знать, чему равна сторона квадрата, площадь или периметр: К примеру, если у нас есть квадрат со сторонами 100 см, то его диагональ будет по формуле √2*a = √2*100 = 1,4142*100 = 141,42 см. Zolotynka 4 года назад Исходя из того, что, согласно теореме Пифагора, диагональ делит квадрат на два конгруэнтных прямоугольных треугольника, мы можем использовать длину стороны квадрата, чтобы найти длину диагонали (которая будет являться гипотенузой треугольника). Следовательно, d=b√2, где d — длина диагонали, а b — длина одной из сторон. ** Например, если длина стороны квадрата 5 сантиметров, то, согласно нашей формуле, длина диагонали будет: d=5√2, или d=5*1,414=7,07. ** Длину диагонали можно узнать, если известны, например, площадь или периметр квадрата. В этом случае придется использовать сразу несколько формул. Так же как и найти гипотенузу у равнобедренного треугольника. Квадрат это правильная геометрическая фигура, имеющая четыре равных стороны. Имея в условии слово «квадрат» можно вообще найти его диагональ по одной стороне, ибо все остальные будут равные ёй. Длину одной из сторон, умножить её на два и возвести в квадрат. Результатом и будет квадрат диагонали. Alexgroovy 4 года назад Диагональ квадрата принято рассчитывать, оперируя понятиями сторона, площадь и периметр. Имея эти данные легко воспользоваться формулами для расчета диагонали квадрата. d = √2 * a, где a — длина стороны квадрата. d = √2S, здесь S — площадь квадрата. d = P / 2√2, где P — периметр. Татьяна-Татьяна 7 лет назад На основании теоремы Пифагора — сумма квадратов катетов равна квадрату гипотенузы. То есть, если сторона квадрата равна «а», то диагональ его («в») равна корню квадратному из выражения (2a^2). То есть вот так: а^2=b^2+b^2 а^2= 2b^2 a=√2b^2 a=b√2 gematogen 6 лет назад Если взять любой квадрат и принять его сторону за букву — a, то диагональ будет равна √2а. Это можно вычислить так же по теореме Пифагора, при которой сторона a*a+a*a=2a*a, из этого извлекаем корень и получаем √2а. Знаете ответ? |
Заключение
Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.
- d = rad2*a;
- d = rad2*radS;
- d = rad2*P/4;
- d = 2*R;
- d = rad2*2*r.
Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.
Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.
![]()
Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.