Периметр и площадь квадрата
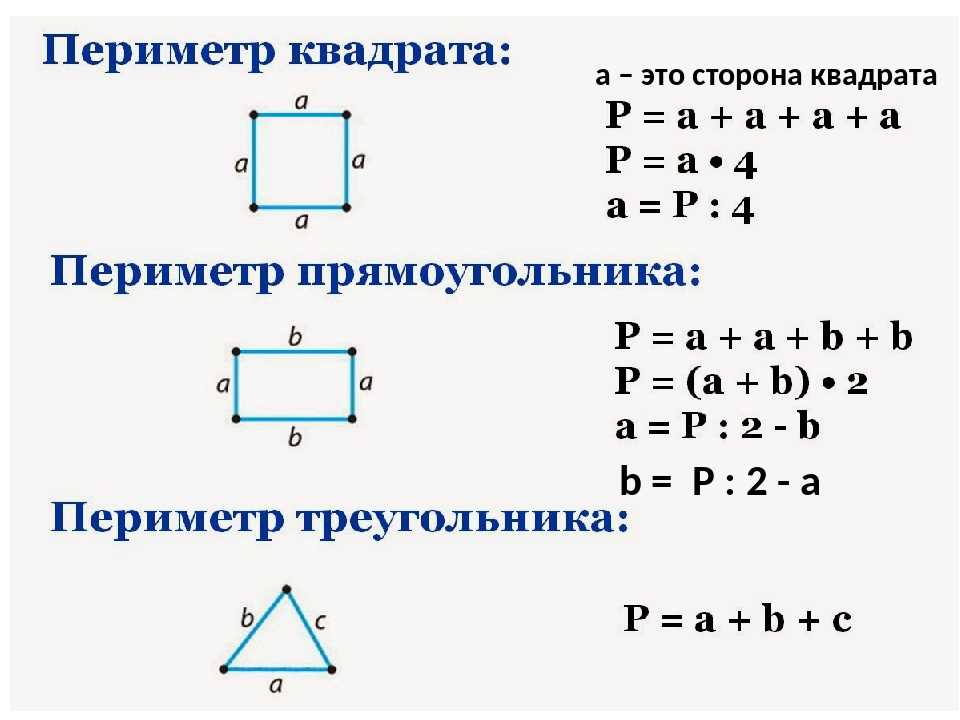
Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:
P= a+a+a+a
Например, перед нами квадрат со стороной 10 см.
Ответ: 40 см
P
= 10+10+10+10
P
=40
Ответ: 40 см
![]()
Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.
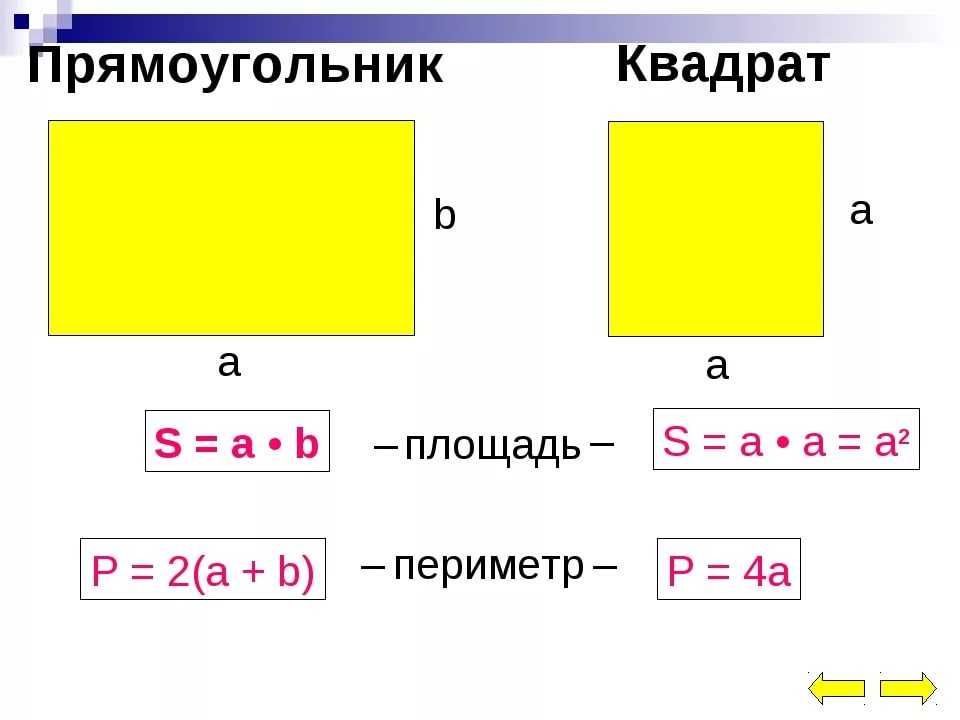
Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:
S – это площадь, а – сторона квадрата.
Например, в задаче указано, что длина стороны квадрата составляет 10см.
S= 100
см 2
Ответ: 10
см 2
![]()
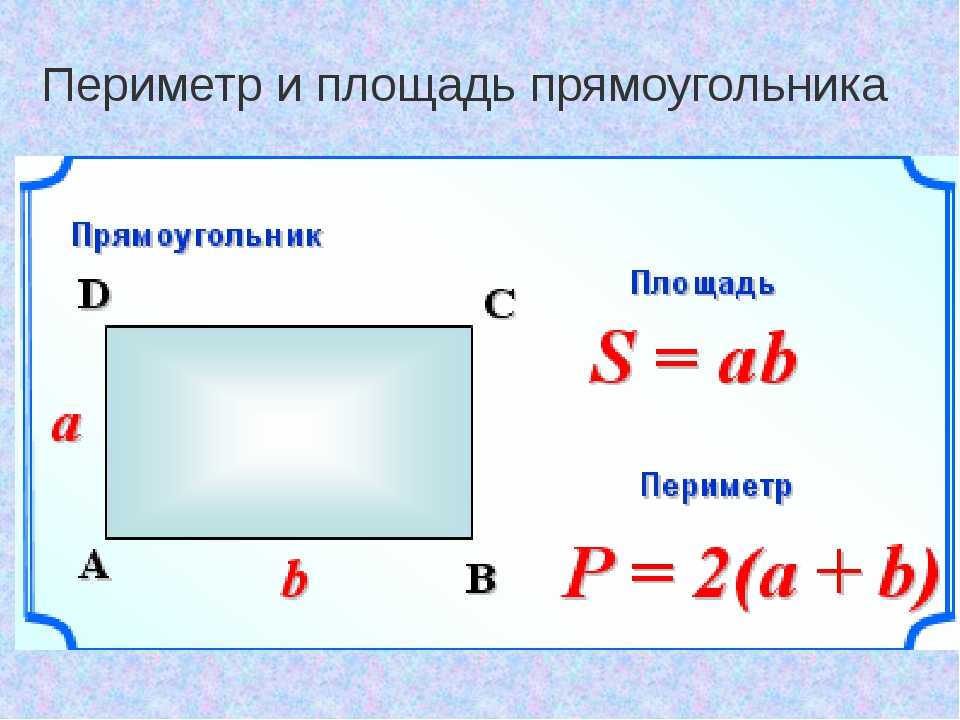
Периметр и площадь прямоугольника
Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:
P= (a+b)*2
Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.
Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.
P
= (6+2) * 2
P
= 16
Ответ: 16 см
![]()
Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:
Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.
S
= 5*2
S
=10см 2
Ответ: 10 см 2
Как найти площадь прямоугольника,если известен периметр и отношение сторон?
Периметр равен сумме длин всех сторон, следовательно, P = 4*a = 4*3 = 12.
ТреугольникЗадача: дан произвольный треугольник ABC, площадь которого равна 14. Найдите периметр треугольника, если проведенная из вершины B высота делит основание треугольника на отрезки длиной 3 и 4 см.Решение: по формуле площадь треугольника – это половина произведения основания на высоту, т.е. S = ½*AC*BE. Периметр равен сумме длин всех сторон. Длину стороны AC найдите, сложив длины AE и EC, AC = 3 + 4 = 7. Найдите высоту треугольника BE = S*2/AC = 14*2/7 = 4.Рассмотрите прямоугольный треугольник ABE. Зная катеты AE и BE, можно найти гипотенузу по формуле Пифагора AB^2 = AE^2 + BE^2, AB = √(3^2 + 4^2) = √25 = 5.Рассмотрите прямоугольный треугольник BEC. По формуле Пифагора BC^2 = BE^2 + EC^2, BC = √(4^2 + 4^2) = 4*√2.Теперь известны длины всех сторон треугольника. Найдите периметр из их суммы P = AB + BC + AC = 5 + 4*√2 + 7 = 12 + 4*√2 = 4*(3+√2).
| Как найти периметр трапеции — wikiHow |
|
Вы можете найти периметр, если вам даны оба основания, высота и оба угла, …. Теперь, когда вам известна площадь треугольника, боковые стороны и …http://ru.wikihow.com/%D0%BD%D0%B0%D0%B9%D1%82%D0%B8-%D0%BF%D0%B5%D1%80%D0%B8%D0%BC%D0%B5%D1%82%D1%80-%D1%82%D1%80%D0%B0%D0%BF%D0%B5%D1%86%D0%B8%D0%B8 |
ОкружностьЗадача: известно, что площадь окружности равна 16*π, найдите ее периметр.Решение: запишите формулу площади окружности S = π*r^2. Найдите радиус окружности r = √(S/π) = √16 = 4. По формуле периметр P = 2*π*r = 2*π*4 = 8*π. Если принять, что π = 3.14, то P = 8*3.14 = 25.12.
Полезен совет?
Источники
Найдите сами
Как найти периметр если известна площадь — версия для печати
Площадь прямоугольника — формула нахождения
Ненамного сложнее вычислить и площадь геометрической фигуры. Площадь принято обозначать буквой S, а измеряют ее в квадратных сантиметрах, миллиметрах или метрах — в отличие от периметра, где используются просто метры, миллиметры и сантиметры.
S = a*b, поэтому для нахождения площади нужно всего лишь знать длину прямоугольника и его ширину — то есть, показатели двух из сторон. Их необходимо умножить между собой и записать ответ в указанных единицах длины.
Еще проще выглядит формула для нахождения площади квадрата. Поскольку стороны геометрической фигуры равны друг другу, показатели длины и ширины будут совпадать. Необходимо взять показатель одной из сторон и возвести его в квадрат. Записывается это следующим образом — S = а2.
При записи решения задач на нахождение периметра или площади рядом с обозначениями Р или S принято ставить маленькие буквенные обозначения конкретной фигуры. Например, Pabcd, или Sabcd. Это позволяет помнить, для какого именно прямоугольника ищется площадь или периметр.
Как найти периметр если известна площадь
Площадь и периметр — основные числовые характеристики любых геометрических фигур. Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных.
Инструкция
ПрямоугольникЗадача: найдите периметр прямоугольника, если известно, что площадь равна 18, а длина прямоугольника в 2 раза больше ширины.Решение: запишите формулу площади для прямоугольника – S = a*b. По условию задачи b = 2*a, отсюда 18 = a*2*a, a = √9 = 3. Очевидно, что b = 6. По формуле периметр равен сумме всех сторон прямоугольника – P = 2*a + 2*b = 2*3 + 2*6 = 6 + 12 = 18. В данной задаче периметр совпал по значению с площадью фигуры.
| Расчет периметра и площади треугольника — Allbe.org |
|
Здесь Вы можете рассчитать площадь и периметр треугольника. … Задача 2: Найдите периметр треугольника, если известна длина его трех сторон = 1 …http://allbe.org/kalkulyator-ploshhadi-treugolnika/ |
КвадратЗадача: найдите периметр квадрата, если его площадь равна 9.Решение: по формуле площади квадрата S = a^2, отсюда найдите длину стороны a = 3.
Расчет площади фигуры по известной диагонали
![]()
Завершим статью рассмотрением вопроса вычисления площади четырехугольника, вершины прямых углов которого соединены диагональю. Рассчитаем площадь современного ЖК-монитора, если известно, что длина его диагонали с = 35 см.
Решить эту задачу можно потому, что монитор имеет стандартизированное отношение сторон, равное 16:9. Обозначая за x неизвестный коэффициент, получаем длины сторон монитора:
Теперь применяем формулу для определения диагонали, получаем:
Тогда стороны монитора и площадь его равны:
Отметим еще раз, что определить по значению диагонали площадь можно только в том случае, если известно отношение сторон прямоугольника.
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
![]()
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
![]()
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
![]()
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
![]()
Допустим, потребовалось измерить площадь следующей комнаты:
![]()
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
![]()
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.
![]()
Рис. 2. Прямоугольник
AB || CD, BC || AD
2. Противоположные стороны прямоугольника равны.
![]()
Рис. 3. Прямоугольник
AB = CD, BC = AD
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.
![]()
Рис. 4. Прямоугольник
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.
Рис. 5. Прямоугольник
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника равны.
![]()
Рис. 6. Прямоугольник
AC = BD
7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.
![]()
Рис. 7. Прямоугольник
△ABD = △BCD, △ABC = △ACD
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).
![]()
Рис. 8. Прямоугольник
AC2 = AD2+ CD2
9. Диагонали прямоугольника делятся точкой пересечения пополам.
![]()
Рис. 9. Прямоугольник
AO = BO = CO = DO = АС2 = BD / 2
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.
![]()
Рис. 10. Прямоугольник
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.
Рис. 11. Квадрат
AВ = ВC = AD = CD
Как найти периметр квадрата?
Зная, что все стороны данного прямоугольника равны, необходимо сделать следующие манипуляции, чтобы вычислить его периметр:
- сложите все четыре стороны квадрата (8 + 8 + 8 + 8 = 32);
- полученное значение будет периметром квадрата, зафиксированным в метрах.
Все формулы и исчисления, приведенные в рамках данной статьи, применимы для любого прямоугольника
Важно помнить, что когда речь идет о других прямоугольниках, которые не являются правильными, значение сторон будет разным, например 4 и 8 метров. Это означает, что для нахождения площади такого прямоугольника необходимо будет умножать разные по значению стороны фигуры, а не одинаковые
Необходимо помнить и то, что площадь измеряется в квадратных, а периметр в простых метрах. Если периметр нарисовать в виде одной длинной линии, то его значение не изменится, что говорит о том, что исчисления проводятся в одномерном пространстве.
Площадь измеряется в двухмерном пространстве, о чем говорят квадратные метры, которые мы получаем, умножив метры на метры. Площадь является индикатором наполненности геометрической фигуры, и говорит нам о том, сколько воображаемого покрытия необходимо для того чтобы заполнить квадрат или другой прямоугольник.
Простые объяснения видео урока позволят быстро вычислить площадь и периметр не только квадрата, но и любого прямоугольника. Данные знания школьного курса будут полезны во время ремонта дома или на садовом участке.
Как найти площадь прямоугольника если известен периметр
По условию задачи b = 2*a, отсюда 18 = a*2*a, a = ?9 = 3. Очевидно, что b = 6. По формуле периметр равен сумме всех сторон прямоугольника – P = 2*a + 2*b = 2*3 + 2*6 = 6 + 12 = 18. В данной задаче периметр совпал по значению с площадью фигуры.
КвадратЗадача: найдите периметр квадрата, если его площадь равна 9.Решение: по формуле площади квадрата S = a^2, отсюда найдите длину стороны a = 3. Периметр равен сумме длин всех сторон, следовательно, P = 4*a = 4*3 = 12.
ТреугольникЗадача: дан произвольный треугольник ABC, площадь которого равна 14. Найдите периметр треугольника, если проведенная из вершины B высота делит основание треугольника на отрезки длиной 3 и 4 см.Решение: по формуле площадь треугольника – это половина произведения основания на высоту, т.е. S = 1/2 *AC*BE. Периметр равен сумме длин всех сторон. Длину стороны AC найдите, сложив длины AE и EC, AC = 3 + 4 = 7. Найдите высоту треугольника BE = S*2/AC = 14*2/7 = 4.Рассмотрите прямоугольный треугольник ABE. Зная катеты AE и BE, можно найти гипотенузу по формуле Пифагора AB^2 = AE^2 + BE^2, AB = ?(3^2 + 4^2) = ?25 = 5.Рассмотрите прямоугольный треугольник BEC. По формуле Пифагора BC^2 = BE^2 + EC^2, BC = ?(4^2 + 4^2) = 4*?2.Теперь известны длины всех сторон треугольника. Найдите периметр из их суммы P = AB + BC + AC = 5 + 4*?2 + 7 = 12 + 4*?2 = 4*(3+?2).
ОкружностьЗадача: известно, что площадь окружности равна 16*?, найдите ее периметр.Решение: запишите формулу площади окружности S = ?*r^2. Найдите радиус окружности r = ?(S/?) = ?16 = 4. По формуле периметр P = 2*?*r = 2*?*4 = 8*?. Если принять, что ? = 3.14, то P = 8*3.14 = 25.12.
Внимание, только СЕГОДНЯ!
Классификация
Прямоугольник — это частный случай параллелограмма и трапеции . Квадрат является частным случаем прямоугольника.
Традиционная иерархия
Прямоугольник является частным случаем параллелограмма , в котором каждая пара смежных сторон находится перпендикулярно .
Параллелограмм — это особый случай трапеции (известной как трапеция в Северной Америке), в которой обе пары противоположных сторон параллельны и равны по длине .
Трапеция — это выпуклый четырехугольник, у которого есть по крайней мере одна пара параллельных противоположных сторон.
Выпуклый четырехугольник — это
- Просто : граница не пересекает саму себя.
- В форме звезды : весь интерьер виден с одной точки, не пересекая края.
Альтернативная иерархия
Де Вильерс определяет прямоугольник в более общем смысле как любой четырехугольник с осями симметрии, проходящими через каждую пару противоположных сторон. Это определение включает как прямоугольные прямоугольники, так и скрещенные прямоугольники. Каждая из них имеет ось симметрии, параллельную и равноудаленной от пары противоположных сторон, а другая — серединный перпендикуляр этих сторон, но в случае скрещенного прямоугольника первая ось не является осью симметрии для обеих сторон. что он делит пополам.
Четырехугольники с двумя осями симметрии, каждая из которых проходит через пару противоположных сторон, относятся к большему классу четырехугольников, по крайней мере, с одной осью симметрии через пару противоположных сторон. Эти четырехугольники состоят из равнобедренных трапеций и скрещенных равнобедренных трапеций (скрещенные четырехугольники с таким же расположением вершин, что и равнобедренные трапеции).
Некоторые геометрические свойства прямоугольника
Поскольку рассматриваемая фигура обладает некоторой симметрией, имеет прямые углы и попарно параллельные стороны, то для нее можно выделить ряд важных свойств, используемых на практике. Перечислим их:
- Всякая прямая, которая проходит через центр C фигуры, пересекает ее в двух точках, находящихся на одинаковом расстоянии от точки C. Максимальное расстояние от C до стороны диагонали прямоугольника равно половине длины его диагонали, минимальное же расстояние равно половине длины его меньшей стороны.
- Если поделить одну сторону прямоугольника точкой пополам, то, соединяя эту точку с вершинами противоположной параллельной стороны, получаем равнобедренный треугольник с площадью, равной половине площади прямоугольника.
- Если точку, описанную выше, смещать из центра стороны к одному или другому ее концу, то равнобедренность отмеченного треугольника будет нарушаться, однако его площадь будет оставаться неизменной.
- Любой прямоугольник можно вписать в окружность.
Первое свойство является очевидным, поскольку любая прямая, проходящая через C, будет пересекать параллельные стороны фигуры. Докажем остальные свойства.
Примеры вопросов и задач
Разберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач.
Задача 1. Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза?
Решение Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a • 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз.
Вопрос 1. Четырёхугольник с прямыми углами — это квадрат?
Решение Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником.
Задача 2. Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ.
https://youtube.com/watch?v=m0Q0oaI-JSQ
Решение: Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16.
Вопрос 2. У прямоугольника все стороны равны или нет?
Решение Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком.
Задача 3. Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.
![]() Решение По формулам для квадрата проведём следующие расчёты:
Решение По формулам для квадрата проведём следующие расчёты:
- Определим, чему равны основные элементы квадрата: a = √ S = √289 = 17, d = a √2 =1 7√2.
- Подсчитаем, чему равен радиус описанной вокруг четырёхугольника окружности: R = 0,5 d = 8,5√2.
- Найдём радиус вписанной окружности: r = a / 2 = 17 / 2 = 8,5.