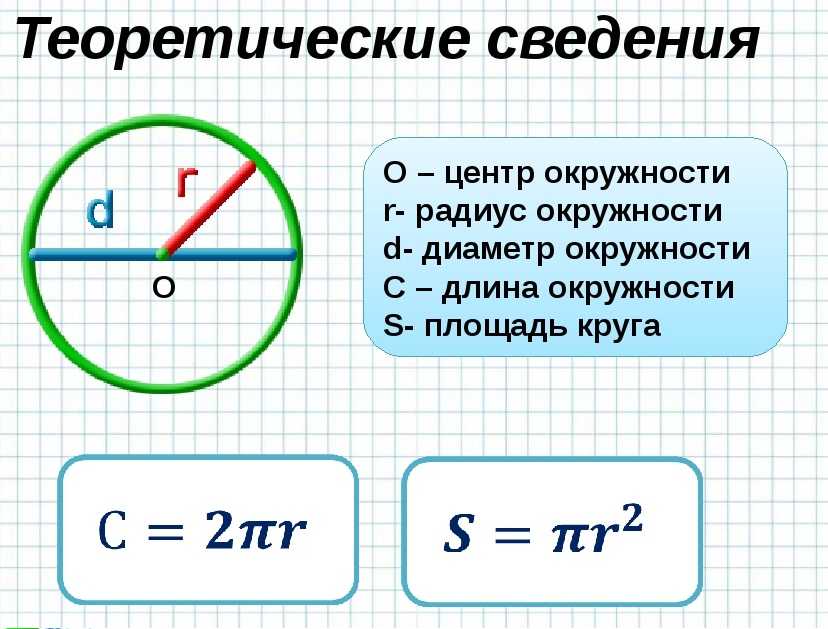
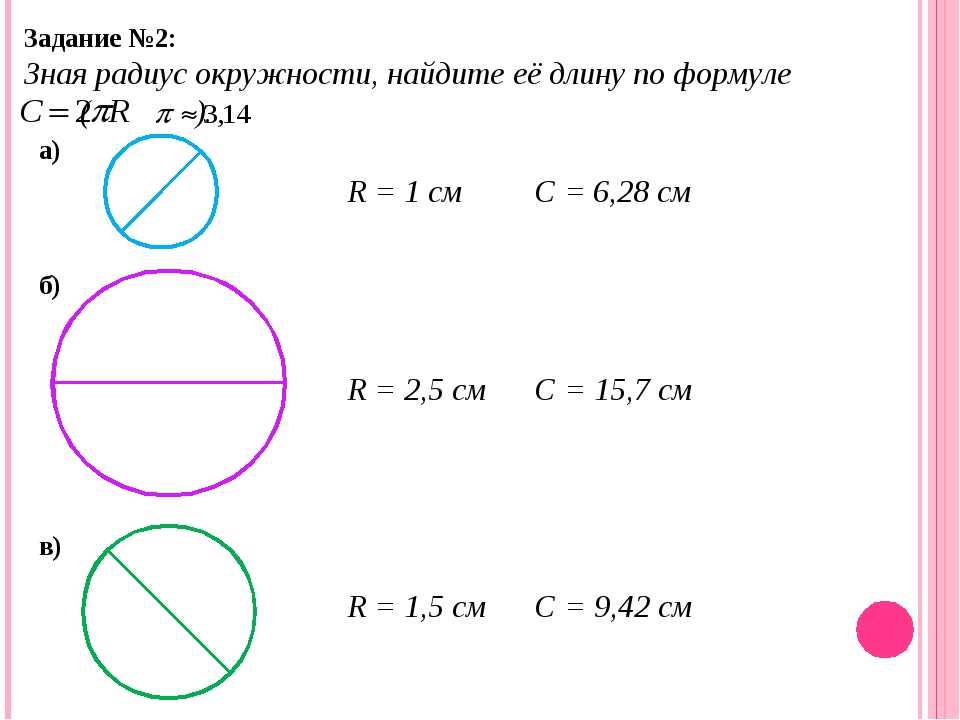
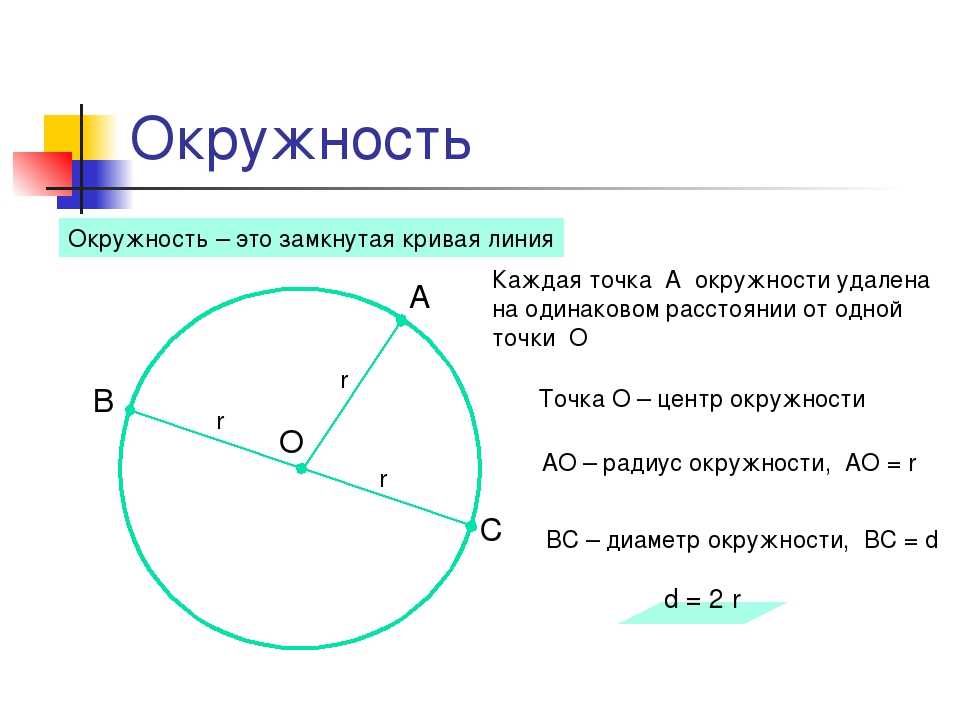
Что такое радиус
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Вот так это выглядит графически .
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или « спица колеса ». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин . А потому и продолжим говорить именно о нем.
Диаметр круга
Нарисуйте две окружности с радиусом 3 см. Фигуру справа закрасьте желтым карандашом. Получится круг.В обеих фигурах проведите диаметры и радиусы.
![]()
Измерьте диаметр окружности и диаметр круга. Сколько у вас получилось?
Правильно, 6 см. Радиус круга равен 3 см. Он два раза помещается в диаметре, значит это половина или одна вторая доля от целого.
6 : 3 = 2
Радиус круга равен половине или 1/2 диаметра.
Путем несложных математических вычислений можно понять, что диаметр в 2 раза больше радиуса.
![]()
АВ = АО + ОВ
Решите задачу
Третьеклассник вырезал круг радиусом 50 мм. Сколько сантиметров в его диаметре?
Решение:
50 ∙ 2 = 100 (мм)
100 мм = 10 см
Ответ: диаметр круга равен 10 см.
Вы хорошо справились.
Нам пора провести зарядку для глаз, чтобы сберечь зрение.
Физкультминутка
- Зажмурьтесь, потом откройте глаза шире. Лоб остается гладким без морщин. Повторите упражнение три раза.
- Теперь подойдите к окну, посмотрите вдаль. Внимательно вглядитесь, потом попытайтесь увидеть кончик носа. Получилось? Тогда повторяйте упражнение четыре раза. Не спешите.
- Медленно делайте круговые движения снизу вверх, направо, вниз, влево глазами, как будто вращаете большое колесо, 2 раза в одну сторону. Теперь обратно. Не двигайте головой, следите только глазами.
- Найдите взглядом верхний правый угол комнаты, хлопните в ладоши, опустите взор на кончик носа.Смотрите вверхний левый угол, далее на кончик носа. Повторите пять раз.
- Прикройте глаза, 10 секунд постойте спокойно, ровно неглубоко подышите.
Ребята, я тоже люблю укреплять здоровье. Вчера пошел на хоккейную площадку. Но вместо игры попросили начертить круги больших диаметров, чтобы обновить разметку поля.
Задача 1
Как начертить без циркуля круг для вбрасывания шайбы диаметром 300 мм?
Решение:
300 мм = 30 см
Радиус круга равен половине диаметра.
30 : 2 = 15 (см)
Возьмите гвоздь, карандаш, нитку длиной 15 см. Начертите окружность как показано на рисунке.
![]()
Задача 2
Из центра поля нужно нарисовать круг синей краской диаметром 9 метров.
Рассуждаем: диаметр круга 9 м, значит радиус — половина.
9 м = 900 см
900 : 2 = 450 (см) = 4 м 50 см.
На центральную точку встает друг Гвоздик, крепко держит конец веревки, а к другому концу нужно закрепить кисть с краской. Фиксик Игрек на коньках едет вокруг Гвоздика, рисует линию окружности. Главное — туго натягивать веревку, чтобы радиус в 450 см не уменьшался. Вот такая разметка получается в центре хоккейной площадки:
![]()
После работы пора поиграть в хоккей.
Похожим способом можно начертить 7 окружностей больших диаметров на картоне для новогодней елки. Посмотрите на рисунок, какая красавица получается.
Поделку делайте вместе с родителями. Для больших кругов возьмите карандаш, гвоздик и нитку. Маленькие — нарисуйте циркулем. Понадобится начертить всего 11 окружностей для десяти обручей елки.
![]()
Задача 3
Диаметр первого нижнего круга елки равен 80 см, а каждого следующего уменьшается на 8 см. Найдите, чему равны диаметры следующих кругов.
Какой диаметр маленького круга наверху у елки?
Для решения задачи вспомните таблицу умножения на 8.
Обратный отсчет диаметров круга по таблице 80, 72, 64, 56, 48, 40, 32, 24, 16, 8.
Диаметр маленького круга 8 см.
Вы отлично выполнили вычисления.
Теперь отгадайте новую загадку. Что идет, не двигаясь с места? (Правильно, это время.)
По площади сектора и центральному углу
-
Запишите формулу для вычисления площади сектора.
-
2
В формулу подставьте значения площади сектора и центрального угла. Эти значения должны быть даны в задаче. Убедитесь, что известна площадь сектора, а не площадь круга. Значение площади сектора подставляется вместо переменной , а значение центрального угла вместо переменной
Например, если площадь сектора равна 50 см2, а центральный угол равен 120 градусов, формула запишется следующим образом: .
.
-
3
Разделите центральный угол на 360. Так вы определите, какую часть круга занимает сектор.
-
4
Изолируйте .
Например:
Для этого разделите обе части формулы на обыкновенную дробь или десятичную дробь, равную части, которую занимает сектор на круге. Если вы не пользуетесь калькулятором, делите на обыкновенную дробь. С помощью калькулятора можно разделить на десятичную дробь, но помните, что чем меньше цифр после десятичной запятой, тем менее точный результат вы получите.
-
5
Разделите обе части формулы на . Так вы изолируете переменную . Чтобы получить более точный результат, воспользуйтесь калькулятором. Число
Например:
округлите до 3,14159 или до 3,14.
Как найти радиус описанной окружности
Предположим, что a, b, c – это стороны треугольника. Если знать их величины, то можно найти радиус описанной вокруг него окружности. Для этого сначала нужно найти полупериметр треугольника. Чтобы было легче для восприятия, обозначим его маленькой буквой p. Он будет равен половине суммы сторон. Его формула: p = (a + b + c) / 2.
Также вычислим произведение длин сторон. Для удобства обозначим его буквой S. Формула радиуса описанной окружности будет выглядеть так: R = S / (4 * √(p * ( p — a ) * (p — b) * (p — c)).
Рассмотрим пример задачи. У нас есть окружность, описанная вокруг треугольника. Длины ее сторон составляют 5, 6 и 7 см. Сначала вычисляем полупериметр. В нашей задаче он будет равен 9 сантиметрам. Теперь вычислим произведение длин сторон – 210. Подставляем результаты промежуточных расчетов в формулу и узнаем результат. Радиус описанной окружности равен 3,57 сантиметра. Записываем ответ, не забывая о единицах измерения.
Основные характеристики окружности
1. Радиус — это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.
2. Хорда — это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD — хорды окружности с центром в точке О.
3. Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр — это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN — диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.
4. Дуга — это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC — дуги, ограниченные точками К и С.
Как найти площадь круга через длину окружности
Для начала вспомним, как вычисляется длина окружности. Здесь, как и в других формулах для круга и окружности используется постоянная π. Нужно запомнить, что в математике и физике этот символ является непременным участником всех вычислений, связанных с кругом, окружностью, циклическими процессами, движением по дуге. В частности, длину окружности находим по формулам L=2 πR, или L= πD. Используя их, находим:
R=L/2 π; (1)
D=Lπ. (2)
Используя запись 1 в формуле S = π∙r2 получаем:
S = π(L/2 π)2 = L/4 π.
Аналогичный результат получим, используя формулу 2.
Как вычислить площадь круга, описанного вокруг правильного многоугольника
В каждый круг легко вписать любой правильный многоугольник. Рассмотрим случаи с самыми простыми фигурами. Если в круг вписан квадрат, то формула будет выглядеть так:
S=2π⋅a2/2, где а – сторона квадрата.
Если в круг вписан равносторонний (правильный) треугольник, то формула будет выглядеть так:
S=π⋅a2/3.
Если в равностороннем треугольнике неизвестна длина стороны, но известна высота, то используем формулу:
S=π⋅(2⋅h/3)2.
Если треугольники неправильные, например, равнобедренные или разносторонние, то формулы получаются сложнее. Например, для вычисления площади по данным равнобедренного треугольника используется формула:
S=π⋅( a4/4⋅a2−b2)
В случае прямоугольного треугольника, мы используем формулу:
S=π/4⋅(a2+b2).
Если круг описан вокруг равнобедренной трапеции, то рассчитать площадь можно по более сложной формуле:
S=π⋅( a⋅d⋅c/4⋅√p⋅(p−a)⋅(p−d)⋅(p−c)).
Как видим, задачу вычисления площади круга можно решить при помощи готовых формул, рассчитанных практически для любого случая, используя вписанные или описанные простые геометрические фигуры. Приведем еще несколько из готовых формул, на этот раз, для фигур, внутри которых находится круг неизвестного радиуса:
S=π⋅a2/12 – для равностороннего треугольника;
S=π⋅b2/4⋅(tgα/2)2 — для равнобедренной трапеции;
S=π⋅(а/2)2=π⋅а2/4 — для квадрата.
Учитывая небольшой объем статьи, все формулы приводим без доказательств, как руководство для практического использования при решении геометрических или технических задач.
Часто возникает проблема определения площади полукруга. Это можно сделать очень просто, вычислив площадь полного круга и разделив ее на 2. Если использовать формулу, то выглядеть это будет так:
S = π∙r2/2, или
S= π∙ D2/4/2 = S= π∙ D2/8.
Для решения практических задач сложно пользоваться формулами, да и времени для этого найти не всегда получается. Лучше всего воспользоваться онлайн-калькуляторами на специализированных сайтах
Здесь важно правильно замерить нужные параметры в требуемых единицах. Нот для учеников и студентов такие сервисы не подходят — легкое получение готового результата отучает мыслить самостоятельно и никак не углубляет знаний
Длина и площадь окружности через радиус
Об этих математических величинах мы решили рассказать не случайно. Дело в том, что при их вычислении просто необходимо знать значение радиуса. И наоборот, зная длину окружности или ее площадь, можно найти радиус.
Длина окружности
Длина окружности – это кривая, которая состоит из точек, равноудаленных от центра окружности. Проще говоря, это длина поверхности окружности.
Длина окружности одновременно является и ее периметром , а потому в геометрии она обозначается латинской буквой «Р» (иногда встречаются и «L», и «C»). А формула для ее вычисления выглядит следующим образом:
Иногда ее пишут и как P=πD, так как 2R – это удвоенный радиус, что, как мы уже сказали выше, является диаметром. Но классическая формула во всех учебниках дается все-таки через радиус.
Гораздо интереснее здесь рассмотреть величину, обозначаемую буквой π. Это как многим известно, математическая постоянная. Она произносится как « Пи» и равна 3,14 .
Хотя на самом деле количество знаков после запятой у «пи» не ограничено. Но для простоты вычислений решено брать именно так.
Площадь окружности
Площадь окружности – это пространство, которое находится внутри ее периметра. Она обозначается латинской буквой «S». А формула для ее вычисления выглядит так:
Опять же, здесь R- это радиус, а π – математическая постоянная, равная 3,14.
![]()
Понятие доли
Вы когда-нибудь заглядывали в тетради к старшеклассникам? Смотрите, какой у меня пример.
![]()
Видите сложение, вычитание, умножение? Знаки этих действий известны: плюс, минус, точка. Деление же в примере обозначено горизонтальной чертой.На рисунке она выделена красным цветом. Я расскажу, когда в математике используют черту.
Мы умеем делить несколько предметов, но часто деление нужно, чтобы раздробить одно число на равные части — доли от целой величины.
Один разделить на два — это одна вторая. Что же это такое?
В жизни вы часто так делали. Например, один апельсин делили с другом: брали нож и разрезали его пополам.
![]()
Каждый из вас получал половину или одну долю.
На лесной полянке собралось девять друзей, апельсин делили на всех. Рассмотрите рисунок. Как называется каждая часть фрукта?
![]()
Совершенно верно, это долька. Апельсин поделили на 9 одинаковых долек.Каждая 1 долька апельсина — это одна из девяти равных долей целого фрукта.
Вы теперь поняли, ребята, что в жизни человеку приходится не только пересчитывать предметы, но и делить (дробить) целое на части, вот так появилось в математике понятие доли и дроби.
Знак доли (дроби) обозначают дробной горизонтальной или наклонной чертой. Например, так — 1/9 (одна девятая). Запись придумали арабы в 16 веке.
Доли называют по количеству частей раздробленного одного предмета:
- Разделите, например, яблоко на две равные части, у вас получится название доли «половина» или 1/2 (одна вторая)
- Разрежьте яблоко на три части. Один кусок — это «треть» — 1/3 (одна третья)
- Разломите на четыре доли — «четверть» — 1/4 (одна четвертая)
![]()
Знание о долях помогает решить задачи.
Запомните правило по математике нахождения доли.Чтобы найти долю от числа надо число разделить на эту долю. В дроби число, на которое делят, записано под чертой и называется знаменателем. То число, которое надо разделить, пишут над чертой. Это числитель.
Задание 1
Найдите пятую долю от числа 25. Это значит, что надо выполнить действие деления.
Привычный пример 25 : 5 можно записать вот таким образом:
![]()
Или так — 25/5. 25 – это числитель, а 5 — знаменатель.
25: 5 = 5
Ответ: одна пятая доля от числа 25 равна пяти.
Задание 2
Чему равна 1/4 доля от полоски длинной 16 см?
Полоску согните пополам, ещё раз пополам. Разверните. На сколько долей линией сгиба разделили полоску? Правильно, на 4.
Закрасьте одну такую долю.
Какую долю вы закрасили? (одну четвёртую)
![]()
16 : 4 = 4(см)
Ответ: длина одной четвертой доли полоски составляет 4 см.
Задание 3
Решите задачи на понятие доли. Рассмотрите рисунки. Какая доля каждой фигуры закрашена серым цветом?
![]()
Рассуждаем так.
На рисунке 1 отрезок разделили на 7 частей.Значит, закрашена одна седьмая (1/7) доля фигуры.
Проверьте:
На следующих рисунках заштрихована 1/16 доля квадрата, 1/6 доля шестиугольника, 1/5 доля круга.
Чтобы разобрать понятие массовой доли, представьте себе килограмм яблок (1000 г), который мама купила своим трем детям.
![]()
Из этого килограмма самому младшему ребенку досталась половина всех яблок (несправедливо, конечно!). Старшему — лишь 200 г, а среднему — 300 г.
Значит, массовая доля яблок у младшего ребенка составит половину, или одну вторую (1/2) массовую долю.
У старшего ребенка будет:
1000 : 200 = 5 — одна пятая (1/5) массовая доля
Далее рассуждаем так:
Младшему ребенку дали половину яблок.
1000 : 2 = 500(г)
Яблоки разделили между детьми по 500г, 200г и 300г. Вы знаете, что 500 — это 5 сотен, 200 — 2 сотни, 300 — 3 сотни.
На сколько сотен разделили все яблоки?
5 сотен + 2 сотни + 3 сотни = 10 сотен.
Сколько граммов будет в одной десятой доле?
1000 : 10 = 100 (г) в одной десятой доле
У среднего ребенка 300 г. Во сколько раз больше, чем 100 г?
300 : 100 = 3
В три раза. Значит, у среднего ребенка будет не одна, а три десятых массовых долей 3/10.
Ребята, вы молодцы. Верное решение.
Радиус круга онлайн
Если всё же возникли сложности и высчитать радиус круга по формулам не получается, то можно воспользоваться онлайн-калькуляторами и узнать нужное значение с помощью них.
Для вычисления радиуса нужно только ввести известное значение длины окружности или площади круга в пустую ячейку и нажать кнопку «вычислить».
Вот так легко и просто можно решить поставленную задачку.
Как найти радиус окружности? Этот вопрос всегда актуален для школьников, изучающих планиметрию. Ниже мы рассмотрим несколько примеров того, как можно справиться с поставленной задачей.
В зависимости от условия задачи радиус окружности вы можете найти так.
Формула 1: R = Л / 2π, где Л – это длина окружности, а π – константа, равная 3,141…
Формула 2: R = √( S / π), где S – это величина площади круга.
Формула 3: R = Д/2, где Д – это диаметр окружности, то есть длина того отрезка, который, проходя через центр фигуры, соединяет две максимально удаленные друг от друга точки.
Как найти радиус описанной окружности
Сначала давайте определимся с самим термином. Окружность называется описанной тогда, когда она касается всех вершин заданного многоугольника. При этом следует заметить, что описать окружность можно только вокруг такого многоугольника, стороны и углы которого между собой равны, то есть вокруг равностороннего треугольника, квадрата, правильного ромба и т.п. Для решения поставленной задачи необходимо найти периметр многоугольника, а также вымерить его стороны и площадь. Поэтому вооружитесь линейкой, циркулем, калькулятором и тетрадкой с ручкой.
Как найти радиус окружности, если она описана вокруг треугольника
Формула 1: R = (А*Б*В) / 4S, где А, Б, В – длины сторон треугольника, а S – его площадь.
Формула 2: R = А / sin а, где А – длина одной из сторон фигуры, а sin а – высчитанное значение синуса противолежащего этой стороне угла.
Радиус окружности, которая описана вокруг прямоугольного треугольника.
Формула 1: R = В/2, где В – гипотенуза.
Формула 2: R = М*В, где В – гипотенуза, а М – медиана, проведенная к ней.
Как найти радиус окружности, если она описана вокруг правильного многоугольника
Формула: R = А / (2 * sin (360/(2*n))), где А – длина одной из сторон фигуры, а n – количество сторон в данной геометрической фигуре.
Как найти радиус вписанной окружности
Вписанной окружность называется тогда, когда она касается всех сторон многоугольника. Рассмотрим несколько примеров.
Формула 1: R = S / (Р/2), где – S и Р – площадь и периметр фигуры соответственно.
Формула 2: R = (Р/2 — А) * tg (а/2), где Р – периметр, А – длина одной из сторон, а – противолежащий этой стороне угол.
Как найти радиус окружности, если она вписана в прямоугольный треугольник
Радиус окружности, которая вписана в ромб
Формула 1: R = 2 * Н, где Н – это высота геометрической фигуры.
Формула 2: R = S / (А*2), где S – это площадь ромба, а А – длина его стороны.
Формула 3: R = √((S * sin А)/4), где S – это площадь ромба, а sin А – синус острого угла данной геометрической фигуры.
Формула 4: R = В*Г/(√(В² + Г²), где В и Г – это длины диагоналей геометрической фигуры.
Формула 5: R = В*sin (А/2), где В – диагональ ромба, а А – это угол в вершинах, соединяющих диагональ.
Радиус окружности, которая вписана в треугольник
В том случае, если в условии задачи вам даны длины всех сторон фигуры, то сначала высчитайте периметр треугольника (П), а затем полупериметр (п):
П = А+Б+В, где А, Б, В – длин сторон геометрической фигуры.
А если, зная все те же три стороны, вам дана еще и площадь фигуры, то можете рассчитать искомый радиус следующим образом.
Формула 2: R = S * 2(А + Б + В)
Формула 3: R = S/п = S / ( А+Б+В)/2), где – п – это полупериметр геометрической фигуры.
Формула 4: R = (п — А) * tg (А/2), где п – это полупериметр треугольника, А – одна из его сторон, а tg (А/2) – тангенс половины противолежащего этой стороне угла.
А ниже приведенная формула поможет отыскать радиус той окружности, которая вписана в равносторонний треугольник.
Формула 5: R =А * √3/6.
Радиус окружности, которая вписана в прямоугольный треугольник
Если в задаче даны длины катетов, а также гипотенуза, то радиус вписанной окружности узнается так.
Формула 1: R = (А+Б-С)/2, где А, Б – катеты, С – гипотенуза.
В том случае, если вам даны только два катета, самое время вспомнить теорему Пифагора, чтобы гипотенузу найти и воспользоваться вышеприведенной формулой.
Радиус окружности, которая вписана в квадрат
Окружность, которая вписана в квадрат, делит все его 4 стороны ровно пополам в точках касания.
Формула 1: R = А/2, где А – длина стороны квадрата.
Формула 2: R = S / (Р/2), где S и Р – площадь и периметр квадрата соответственно.
Единицы времени
Каждый человек хочет понять время. Оно нам нужно, потому что мы живем по режиму, а магазины, библиотеки, вокзалы — по расписанию. Определенное количество дел намечаем сделать в единицу времени.
Давайте познакомимся с единицами измерения времени.
Земля обращается вокруг Солнца за 365 суток. Это год. Один раз в 4 года он увеличивается на сутки, и называется високосным.
![]()
С глубокой древности круг считается символом годовых сезонных циклов: зимы, весны, лета и осени. Рассмотрите рисунок годового круга: он поделен на 4 доли — четыре времени года.
Единица величины каждого времени года делится на 3 месяца.
В году 3 ∙ 4 = 12 месяцев. Месяц — единица времени, за которую Луна обходит планету Земля вокруг.
![]()
В каждом месяце 30 или 31, а в феврале 28 или 29 суток.
Исторически основной единицей для времени были сутки (часто говорят «день»). За одни сутки Земля поворачивается вокруг своей оси.
![]()
В результате деления суток на меньшие временные интервалы возникли часы, минуты и секунды. Сутки – единица времени, равная 24 часам. Один час — это 60 минут. Минута состоит из 60 секунд.
Выполните задания
1. Выразите время в указанных единицах измерения
|
8 ч 25 мин. = … мин. |
95 мин. = … ч … мин. |
|
2 мин. 14 сек. = … сек. |
187 сек. = … мин. … сек. |
Решение:
1 час = 60 мин. Значит, в восьми часах будет в 8 раз больше. Нужно выполнить умножение.
60 ∙ 8 = 480 (мин.)
В 8 часах — 480 минут да еще 25 мин. Действие сложения.
480 + 25 = 505 (мин.)
Ответ: 8 ч 25 мин. = 505 мин.
Дальше решайте аналогично:
2 мин. 14 сек. = 60 ∙ 2 + 14 = 134 сек.
95 мин. = 1 ч 35 мин.
187 сек. = 3 ч. 7 сек.
2. Выберите единицы времени, которые расположены в порядке возрастания
а) час, минута, секунда
б) секунда, минута, час
в) минута, час, секунда
Проверьте себя.
Правильный ответ — б.
3. Автомобиль до Москвы едет 2 суток, а обратно 48 часов. Почему такая разница?
Проверьте себя.
2 сут. = 48 ч. Разницы нет.
Наш урок подходит к концу. Я надеюсь, что вы будете ценить свое время, не будете терять его зря.
Я с вами прощаюсь, а вы проверьте свои знания.
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |
, где R – радиус круга, D – диаметр круга Посмотреть доказательство |
|
| Площадь сектора |
, если величина угла α выражена в радианах Посмотреть доказательство |
|
|
, если величина угла α выражена в градусах Посмотреть доказательство |
||
| Площадь сегмента |
, если величина угла α выражена в радианах Посмотреть доказательство |
|
|
, если величина угла α выражена в градусах Посмотреть доказательство |
| Площадь круга |
|
, где R – радиус круга, D – диаметр круга Посмотреть доказательство |
| Площадь сектора |
|
, если величина угла α выражена в радианах Посмотреть доказательство * * * , если величина угла α выражена в градусах Посмотреть доказательство |
| Площадь сегмента |
|
, если величина угла α выражена в радианах Посмотреть доказательство * * * , если величина угла α выражена в градусах Посмотреть доказательство |
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше — то искомый центр дуги выше на прямой.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
![]()
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
![]()
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
| C | = π. |
| D |
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR,
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.