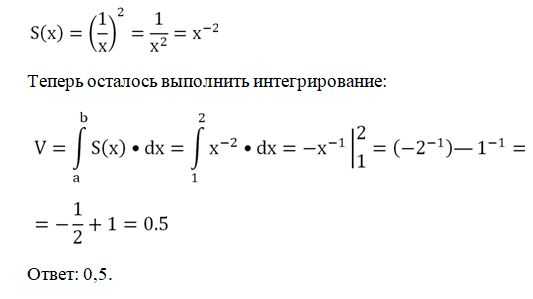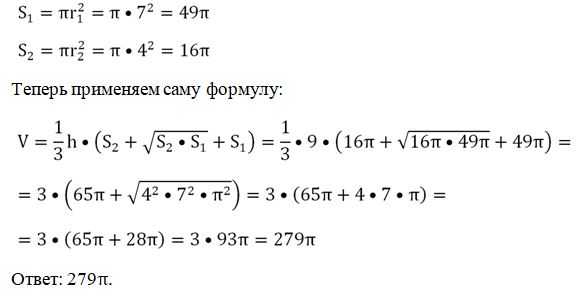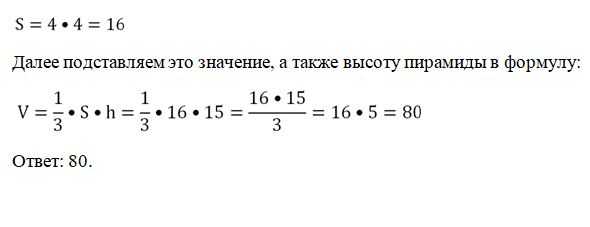Геометрия

Отличие куба от квадрата, разница между ними

Куб и квадрат часто путают, думая, что это тождественные геометрические фигуры. В действительности они отличаются друг от друга, ведь у каждого из этих объектов имеются только им присущие признаки. Какие, нетрудно понять, зная определение куба и квадрата.

Что такое квадрат и что такое куб

Фото: Квадрат

Квадрат – фигура, лежащая на плоскости, и она двухмерная. Её можно отобразить в виде прямоугольника с идентичными по длине сторонами. Квадрат можно вырезать из бумаги.

Фото: Куб

Куб же является трехмерным объектом, имеющим объём и 12 одинаковых граней. Таким образом, это правильный многогранник. Если разложить его на плоскости, то он будет состоять из 6 квадратов. Для наглядности куб можно склеить из плотной бумаги, а лучше слепить из гипса, пластилина.

Фото: разложенный куб на плоскости

В чем разница между кубом и квадратом: сравнение двух фигур

По сравнению с квадратом, куб – более сложная геометрия. Квадрат является фигурой простой, в нём только 4 стороны и 4 угла, между которыми абсолютное равенство. Квадрат можно назвать подвидом прямоугольника, только у которого ширина и длина сторон одинаковы. При этом квадрат всегда плоский. Чтобы посчитать площадь квадрата, достаточно умножить одну его сторону на другую.

Конфигурация куба сложнее, поскольку в нём уже присутствует третья мера – объём. Эта характеристика отражает пространство, которое занимает объект, в нашем случае куб. У куба также есть и третье измерение (параметр) – высота. Между собой ширина, длина и высота у куба равны.

Нахождение объема и площади

Если необходимо посчитать объем фигуры, то для расчета берут длину любого ребра между гранями и возводят её в третью степень. Для нахождения площади трехмерной фигуры куба надо узнать сумму площади всех его сторон. Поскольку они идентичны, то просто площадь одной стороны умножаем на 6. А чтобы найти площадь одной из сторон, умножаем длину ребра на себя же. Допустим, длина ребра 4 см, чтобы найти площадь одной стороны куба, 4 умножаем на 4 – получаем 16. И эту цифру уже увеличиваем в 6 раз. Значит, объём куба будет равен 96 см²

Сложные свойства куба

По сравнению с квадратом куб обладает более сложными, дополнительными характеристиками. Например, геометрический объект имеет четыре сечения, которые представляют собой правильные шестиугольники. Все сечения куба проходят через его центр и располагаются перпендикулярно относительно четырех главных его диагоналей.

Поскольку куб имеет объём, то в него можно вписать различные многогранники – такие как тетраэдр (простейший многогранник с гранями в виде 4-х треугольников), октаэдр (у этого многогранника уже 8 граней), икосаэдр (20 граней многогранника).

Чтобы ещё легче было понять разницу между кубом и квадратом, имеет смысл оценить свойства каждой фигуры наглядно. К примеру, взять обычный детский кубик с наклеенными картинками на его стороны. Так вот, сам кубик – это фигура куб, а каждая наклеенная на его сторону картинка – квадрат.

 876 смотрели,  10 сегодня

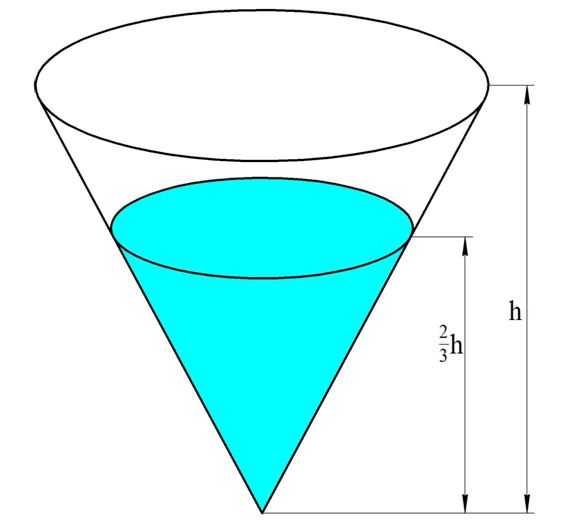
Шаровой сегмент

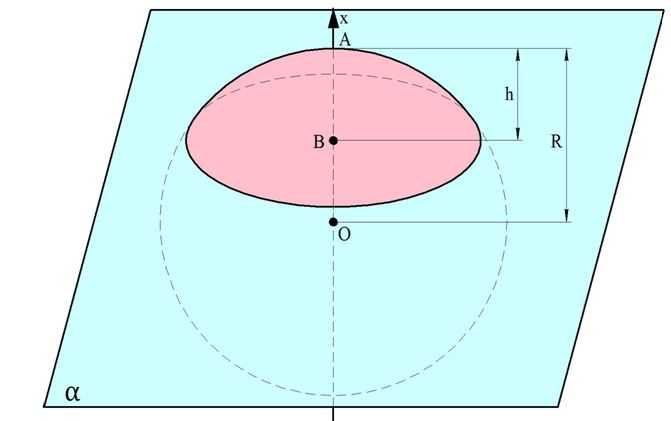
Когда плоскость проходит через шар, она рассекает его на две фигуры, которые именуются шаровым сегментом. Если из центра шара О провести радиус ОА длиной R в направлении плоскости сечения, который перпендикулярен этой плоскости, то он пересечет ее какой-то точке В. Длину отрезка АВ называют высотой шарового сегмента и обозначают буквой h:

Ясно, что при этом отрезок ОВ – это расстояние от секущей плоскости (или от основания сегмента) до центра шара, причем этот отрезок имеет длину R –h.

Можно считать, что шаровой сегмент, как и шар, получается при вращении дуги окружности вокруг оси Ох. Однако если сам шар при этом ограничен плоскостями x = R и х = – R, то сегмент ограничен другими плоскостями: х = R и х = R – h. Это значит, что его объем можно вычислить с помощью интеграла также, как и объем шара, отличаться будет лишь нижний предел интегрирования:

Заметим, что шар можно рассматривать как шаровой сегмент, чья высота вдвое больше его радиуса. И действительно, если в выведенную формулу мы подставим значение h = 2R, то получим уже известную нам формулу объема шара.

Задание. Найдите объем шарового сегмента высотой 6, если он отсечен от шара радиусом 15.

Решение. Используем выведенную формулу:

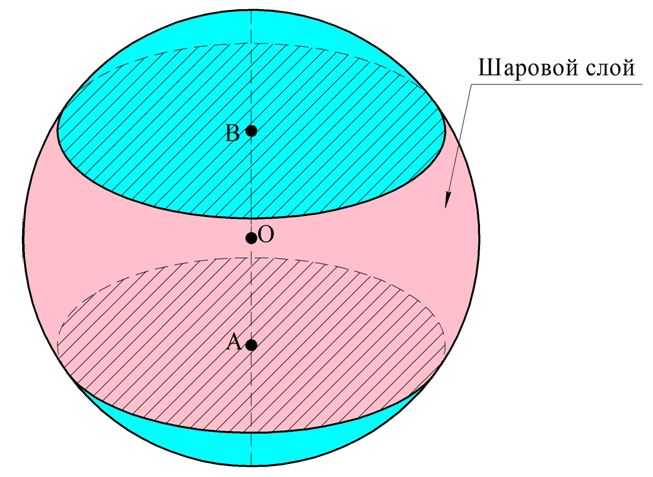
Задание. Диаметр шара разделили на три равных отрезка. Через концы этих отрезков провели секущие плоскости, перпендикулярные диаметру. Чему равен объем тела, заключенного между этими двумя плоскостями (оно называется шаровым слоем), если радиус шара обозначен буквой R?

Решение. Ясно, что для вычисления объема шарового слоя достаточно вычесть из объема шара объемы двух шаровых сегментов, образующихся при проведении секущих плоскостей. Так как они разделили диаметр на три одинаковых отрезка, то высота этих сегментов будет в три раза меньше диаметра шара:

Объем куба и прямоугольного параллелепипеда

Докажем важную вспомогательную теорему:

Действительно, пусть у двух параллелепипедов одинаковы основания. Тогда их можно совместить. Пусть общим основанием будет АВСD, а высотами параллелепипедов будут отрезки АР и АК, причем АР <АК. Объем меньшего параллелепипеда с высотой АР обозначим как V_Р, а большего – как V_K:

Нам надо доказать, что объемы фигур пропорциональны их высотам:

Для начала рассмотрим случай, когда отношение высот является рациональным числом. Это означает, что существует некоторая дробь m/n, такая, что

где m и n – натуральные числа. Тогда разобьем отрезок АК как раз на n равных отрезков. В этом случае отрезок АР будет состоять в точности из m таких отрезков. Далее через концы отрезков проведем плоскости, параллельные основанию:

В результате мы получили n равных параллелепипедов («пластин»), которые все вместе образуют большой параллелепипед объемом V_K. Поэтому объем одной такой пластины равен величине V_K/n:

Итак, мы доказали теорему для случая, когда отношение высот является рациональным числом. Теперь перейдем к более сложному случаю, когда это отношение представляет собой иррациональное число. Здесь можно рассуждать от противного. Предположим, что теорема ошибочна, тогда для каких-нибудь двух параллелепипедов отношение их объемов будет равно не отношению их высот, а какому-то другому числу k:

Это значит, что k либо меньше, либо больше, чем отношение АР/АК. Рассмотрим случай, когда k< АР/АК (случай, когда k> АР/АК, рассматривается аналогичным образом). Тогда возьмем какое-нибудь рациональное число R, находящееся между числами k и АР/АК:

(Примечание. Здесь мы неявно используем утверждение, которое можно доказать в рамках алгебры – между любыми двумя различными действительными числами располагается хотя бы одно рациональное число).

Умножим это неравенство на длину АК:

Построим параллелепипеды с общим основанием АВСD и высотами АК и АР, а также с высотой АЕ = R•АК. Так как R•АК < АР, то точка Е будет лежать между А и Р:

Объем параллелепипеда с высотой АЕ обозначим как V_Е. Ясно, что

ведь число k не может быть одновременно и больше, и меньше R. Полученное противоречие означает, что исходное предположение об ошибочности теоремы неверно, и на самом деле она справедлива, ч. т. д.

Теперь с помощью доказанной теоремы можно вывести известную ещё из младших классов формулу для расчета объема прямоугольного параллелепипеда.Пусть измерения прямоугольного параллелепипеда являются числами а, b и c. Построим:

• единичный куб;
• параллелепипед с габаритами а, 1, 1 с объемом V₁;
• параллелепипед с габаритами а, b, 1 с объемом V₂;
• параллелепипед с габаритами а, b, c с объемом V.

Тогда можно последовательно вычислить их объемы. Объем первого параллелепипеда будет в а раз больше объема единичного куба, то есть он будет равен а. Объем второго параллелепипеда будет больше ещё в bраз, а третьего – ещё в с раз:

Соответственно, для расчета объема параллелепипеда используется формула

Иногда эту формулу формулируют несколько иначе: объем параллелепипеда – это произведение площади его основания на длину высоты, перпендикулярной этому основанию.

Задание. Три смежных ребра прямоугольного параллелепипеда имеют длины 9, 4 и 7 см. Каков объем параллелепипеда?

Решение. Здесь надо просто перемножить габариты параллелепипеда:

Ответ: 252 см3.

Куб можно рассматривать как прямоугольный параллелепипед с одинаковыми измерениями. Поэтому для вычисления его объема надо умножить ребро куба само на себя дважды, то есть возвести его в куб.

Задание. Вычислите объем куба с ребром 8 метров.

Решение. Просто возводим сторону ребро куба в третью степень:

Задание. Если ребро куба увеличить на 2 дм, то его объем вырастет на 98 дм3. Какова длина ребра этого куба?

Решение. Обозначим длину ребра буквой х. Тогда объем куба будет составлять х3 дм. Если ребро увеличить на 2 дм, то оно будет иметь длину х + 2 дм, и тогда объем куба будет равен уже (х + 2)3 дм. Условие задачи можно записать в виде уравнения:

Это квадратное уравнение имеет два корня, 3 и (– 5), что можно проверить с помощью теоремы Виета. Корень х = – 5 не имеет геометрического смысла, поэтому остается ответ х = 3.

Ответ: 3 дм.

Далее рассмотрим перевод единиц измерения объема. Например, как перевести 1 м3 в кубические сантиметры? Рассмотрим куб с ребром 1 м. Ясно, что его объем будет равен 1 м3. С другой стороны, можно сказать, что длина ребра этого куба составляет 100 см:

Тогда объем этого куба можно посчитать так:

Аналогично можно переводить и другие единицы измерения.

Как связан куб с другими фигурами и телами?

Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше. Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником. Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.

Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.

В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.

Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.

Построение гиперкуба

Начнём с начала — с 0-мерного куба. Этот куб содержит 0
взаимно перпендикулярных граней, то есть это просто точка.

1-мерный куб

В одномерном пространстве у нас есть только одно направление.
Сдвигаем точку в этом направление и получаем отрезок.

Это одномерный куб.

2-мерный куб

У нас появляется второе измерение, сдвигаем наш одномерный
куб (отрезок) в направлении второго измерения и получаем квадрат.

Это куб в двумерном пространстве.

С появлением третьего измерения поступаем аналогично:
сдвигаем квадрат и получаем обычный трёхмерный куб.

4-мерный куб (гиперкуб)

Теперь у нас появилось четвёртое измерение. То есть в
нашем распоряжении имеется направление, перпендикулярное
всем трём предыдущим. Воспользуемся им точно так же.
Четырёхмерный куб будет выглядеть вот так.

Естественно, трёхмерный и четырёхмерный кубы нельзя
изобразить на двумерной плоскости экрана. То, что нарисовал я — это проекции.
О проекциях мы поговорим чуть позже, а пока немного голых
фактов и цифр.

Что такое гиперкуб и четырёхмерное пространство

В нашем привычном пространстве три измерения.
С геометрической точки зрения это значит,
что в нём можно указать три взаимно-перпендикулярных
прямых. То есть для любой прямой можно найти вторую,
перпендикулярную первой, а для пары можно найти третью
прямую, перпендикулярную двум первым. Найти четвёртую
прямую, перпендикулярную трём имеющимся, уже не удастся.

Четырёхмерное пространство отличается от нашего
только тем, что в нём есть ещё одно дополнительное направление.
Если у вас уже есть три взаимно перпендикулярные прямые,
то вы можете найти четвёртую, такую, что она будет
перпендикуляра всем трём.

Гиперкуб это просто куб в четырёхмерном пространстве.

Примеры расчетов

Чтобы наглядно продемонстрировать применение приведенных выше правил, рассмотрим несколько конкретных примеров.

В кубометрах

Примеры:

1. Бассейн диаметром 3 м планируется наполнить на глубину 1,5 м. Чтобы определить объем, воспользуемся формулой: V = π * D2/4 * H = 3,14 *32 /4 * 1,5 = 10,5975 м3.
2. При величине радиуса круглой чаши 5 м и высоте бортов 2 м в резервуар можно максимально залить: V = π * R2 * H = 3,14 * 52 * 2 = 157 м3.
3. Допустим, что минимальная высота наполнения составляет 80 см, а глубина на другой стороне 120 см. При диаметре бассейна 300 см получаем: H_ср = (H₁ + H₂)/2 = (80 + 120)/2 = 100 см, V= 3002 * 100 * 0,78 = 7 020 000 (см3) = 7,020 м3.

Справка. В одном кубометре (1 м3) содержится 106 кубических сантиметров воды.

В литрах

Линейные величины традиционно измеряют в метрах и сантиметрах, а жидкости в литрах. Один литр воды теоретически представляет собой кубик со стороной 10 см. В 1 м3 таких кубиков 1000 штук. Таким образом: 1м3 = 1000 литров.

Масса такого объема воды равна 1 тонне.

Примеры:

1. Определим вместимость конструкции диаметром 1 м и глубиной 0,5 м: V = π * D2/4 * H = 3,14 * 12 /4 * 0,5 = 0,3925 м3. Чтобы получить объем в литрах, умножаем на тысячу: V = 392,5 л.
2. Большой резервуар шириной 500 см и глубиной 200 см способен принять: V = D2 * H * 0,78 = 5002 * 200 * 0,78 = 39 000 000 (см3) = 39 тыс.л.
3. Овальный бассейн с длиной 10 м и шириной 4 м, заполненный на 1,5 м, обсчитывается следующим образом: S =π*ab = 3,14 * (10/2) * (4/2) = 31,4 (м2), V = S * H = 31,4 * 1,5 = 47,1 (м3) = 47 100 л.

Вычисление объема тел вращения

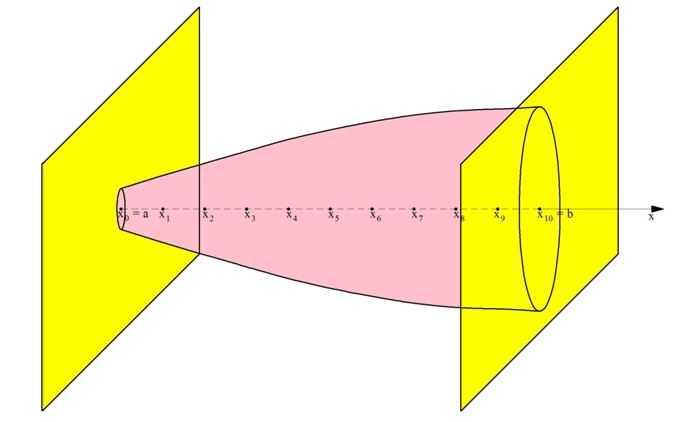
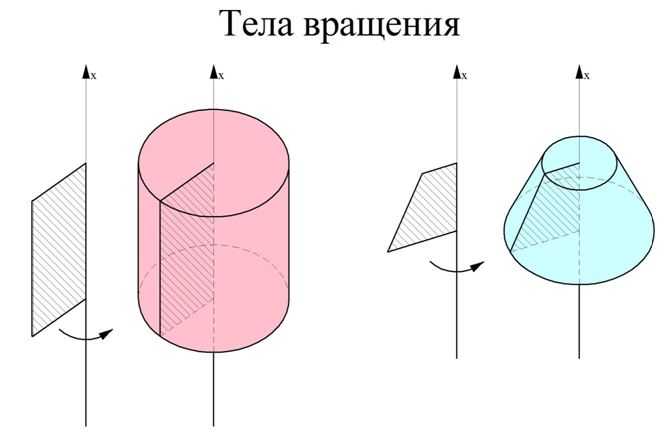
Телом вращения называют тело, которое может быть получено вращением какой-то плоской фигуры относительно некоторой оси вращения. Например, цилиндр получают вращением прямоугольника вокруг одной из его сторон, а усеченный конус – вращением прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

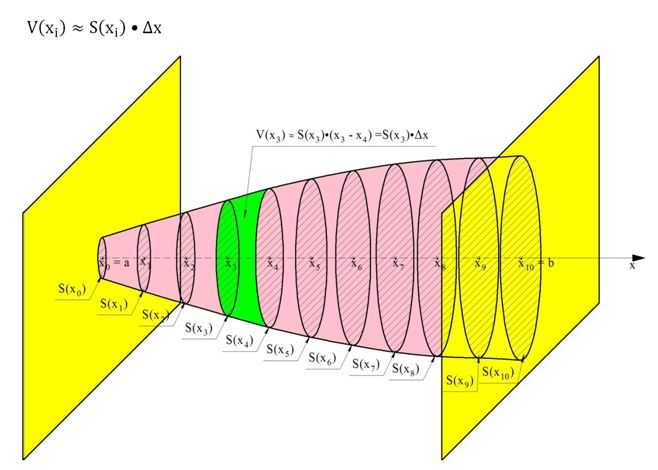
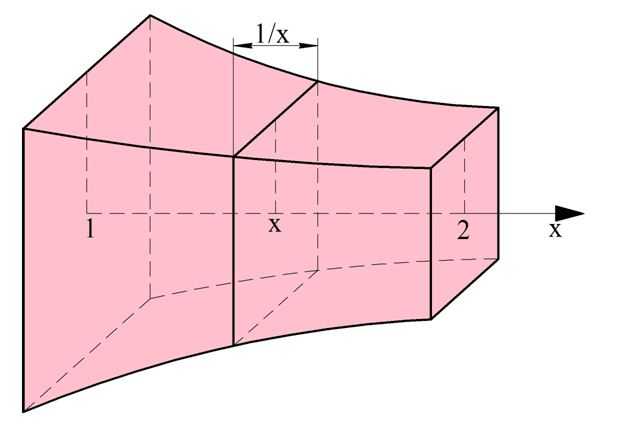
В задачах на вычисление объемов таких тел ось координат Ох уже задана естественным образом – это ось вращения тела. Ясно, что каждое сечение тела, перпендикулярное оси вращения, будет являться кругом.

Рассмотрим случай, когда вокруг оси Ох поворачивают график некоторой функции у = f(x), ограниченный прямыми х = а и у = b. Тогда получится тело, сечениями которого являются круги, причем их радиусы будут равны величине f(x). Напомним, что площадь круга вычисляют по формуле:

Рассмотрим, как на практике используется эта формула.

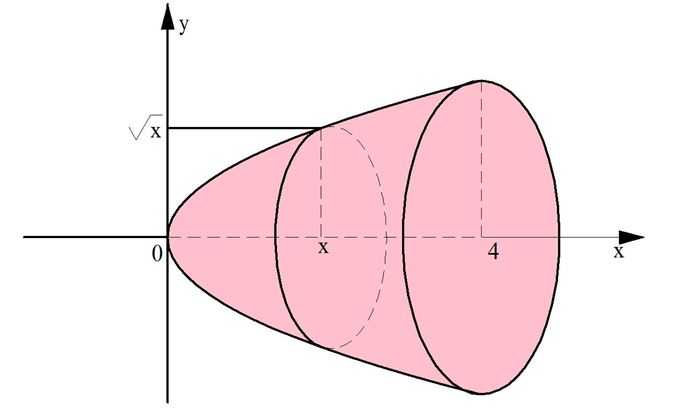
Задание. Объемное тело получено вращением ветви параболы

вокруг оси Ох. Оно ограничено плоскостями х = 0 и х = 4. Каков объем такой фигуры?

Решение. Здесь пределами интегрирования, то есть числами а и b, будут 0 и 4. Используем формулу для тела вращения:

Развёртки

Итак, житель четырёхмерного пространства может увидеть
трёхмерный объект одновременно со всех сторон.
Можем ли мы одновременно со всех сторон увидеть трёхмерный
куб? Глазом — нет. Но люди придумали способ, как
изобразить на плоском рисунке все грани трёхмерного куба одновременно.
Такое изображение называется развёрткой.

Развёртка трёхмерного куба

Как образуется развёртка трёхмерного куба все наверно знают.
Этот процесс показан на анимации.

Для наглядности края граней куба сделаны полупрозрачными.

Следует отметить, что мы способны воспринять эту двумерную картинку
только благодаря воображению. Если рассмотреть фазы разворачивания
с чисто двумерной точки зрения, то процесс будет казаться странным
и совсем не наглядным.

Он выглядит, как постепенное появление сперва очертаний
искажённых квадратов, а потом их расползание на свои места
с одновременным принятием необходимой формы.

Если смотреть на разворачивающийся куб в направлении
одной из его граней (с этой точки зрения куб выглядит как
квадрат), то процесс образования развёртки ещё менее нагляден.
Всё выглядит как выползание квадратов из начального квадрата
(не развёрнутого куба).

Но не наглядна развёртка только для глаз. Как раз
благодаря воображению из неё можно почерпнуть много информации.

Развёртка четырёхмерного куба

Сделать анимированный процесс разворачивания гиперкуба
хоть сколько нибудь наглядным просто невозможно. Но этот
процесс можно представить. (Для этого надо посмотреть на него
глазами четырёхмерного существа.)

Развёртка выглядит так.

Здесь видны все восемь кубов, ограничивающих гиперкуб.

Одинаковыми цветами покрашены грани, которые должны совместиться
при сворачивании. Серыми оставлены грани для которых парных не видно.
После свёртки самая верхняя грань верхнего куба должна совместиться
с нижней гранью нижнего куба. (Аналогично сворачивается развёртка
трёхмерного куба.)

Обратите внимание, что после свёртки все грани восьми кубиков
придут в соприкосновение, замкнув гиперкуб. И наконец, представляя
процесс свёртывания, не забывайте, что при свёртывании происходит не наложение
кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области

Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты
фигурируют в очень многих его картинах. На картине
«Распятие» (1954)
используется развёртка гиперкуба.

Формула площади поверхности куба

П»Ã¾ÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð â ÃÂÃÂþ ÃÂÃÂüüð ÿûþÃÂðôõù òÃÂõàõóþ óÃÂðýõù:

S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6

S=S1âÂÂ+S2âÂÂ+S3âÂÂ+S4âÂÂ+S5âÂÂ+S6âÂÂ

ÃÂûþÃÂðôàúðöôþù óÃÂðýø þôøýðúþòð, ÃÂþ õÃÂÃÂÃÂ:

S1=S2=S3=S4=S5=S6=Sâ²S_1=S_2=S_3=S_4=S_5=S_6=SâÂÂ

S1âÂÂ=S2âÂÂ=S3âÂÂ=S4âÂÂ=S5âÂÂ=S6âÂÂ=Sâ²

Sâ²SâÂÂ

Sâ² â ÿûþÃÂðôàûÃÂñþù óÃÂðýø úÃÂñð.

âþóôð ÿþûýðàÿûþÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð ÷ðÿøÃÂõÃÂÃÂàúðú:

àðÃÂÃÂüþÃÂÃÂøü ýð ÿÃÂøüõÃÂðàÃÂð÷ýÃÂõ ÃÂÿþÃÂþñàòÃÂÃÂøÃÂûõýøàÿþûýþù ÿûþÃÂðôø ÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð.

ÃÂûþÃÂðôàúðöôþù óÃÂðýø úÃÂñð òÃÂÃÂøÃÂûÃÂõÃÂÃÂàúðú ÿûþÃÂðôàúòðôÃÂðÃÂð, ÃÂþ ÃÂÃÂþÃÂþýþù ÃÂõñÃÂð úÃÂñð ÿþ ÃÂþÃÂüÃÂûõ:

Sâ²=aâÂÂa=a2SâÂÂ=acdot a=a^2

Sâ²=aâÂÂa=a2

aa

a â ÃÂÃÂþÃÂþýð úÃÂñð.

ÃÂÃÂÃÂÃÂôð, þúþýÃÂðÃÂõûÃÂýþ ÿûþÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð:

Шаги

Метод 1 из 2:

Вычисление объема прямоугольного предмета (в кубических сантиметрах)

1. 1

   Измерьте длину, ширину и высоту предмета (в сантиметрах). Для этого измерьте требуемые величины с помощью линейки или рулетки или конвертируйте известные вам значения в сантиметры.
   X
   Источник информации

   Например, если вы хотите узнать объем холодильника, найдите его длину, ширину и высоту (в сантиметрах). Предположим, что ваш холодильник в высоту имеет 100 см, в ширину — 50 см, в длину — 40 см.

2. 2

   Запишите высоту предмета.

   В нашем примере запишите, что высота = 100 см.

   Вы можете перемножать величины в любом порядке. Например, начните с высоты.

3. 3

   Умножьте высоту на ширину. Затем умножьте первую величину на какую-нибудь из оставшихся (любую). Например, умножьте высоту на ширину.
   X
   Источник информации

   В нашем примере, умножьте 100 на 50: 100 × 50 = 5000.

4. 4

   Умножьте полученный результат на длину предмета.

   В нашем примере, умножьте 5000 на 40: 5000 × 40 =Н 200 000.

   Последний шаг — умножьте полученный результат на оставшуюся величину. Например, умножьте произведение высоты и ширины на длину.

5. 5

   Запишите ответ в кубических сантиметрах, чтобы он был понятен любому человеку.

   • Единицы измерения записываются так:
     • кубические сантиметры
     • сантиметров в кубе
     • см^3
     • см3

Метод 2 из 2:

Вычисление объема других фигур

1. 1

   Объем куба V= L3, где V — объем, L — сторона. Куб — прямоугольный параллелепипед, у которого все стороны равны.
   X
   Источник информации

   

   

   

   

   

   

   

   

   

   

   Таким образом, формулу для вычисления объема куба можно записать в виде: длина × ширина × глубина = длина × длина × длина = длина3. Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.

2. 2

   Объем цилиндра V = hπr2, где V — объем, h — высота, r — радиус цилиндра. Цилиндр — геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными круглыми плоскостями.
   X
   Источник информации

   Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.

3. 3

   Объем конуса V = (1/3)hπr2, где V — объем, h — высота, r — радиус конуса. Конус — тело с круглым основанием и вершиной над ним. Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.
   X
   Источник информации

4. 4

   Объем шара V = 4/3πr3, где V — объем, r — радиус шара. Шар — абсолютно круглое тело.
   X
   Источник информации

   Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.

• Если вы не уверены в правильности ваших вычислений, проверьте ответ, воспользовавшись калькулятором или помощью другого человека, разбирающегося в математике.
• Кубические сантиметры — единица измерения объема, то есть количественной характеристики пространства, занимаемого телом.
• Для точного измерения величин используйте линейку или рулетку (особенно если вы делаете важные измерения).

Объем шара

Пришло время разобраться и с таким телом, как шар. Здесь можно использовать тот же метод интегрирования, что и в случае с конусом и пирамидой. Но можно поступить и иначе – использовать выведенную нами для тел вращения формулу

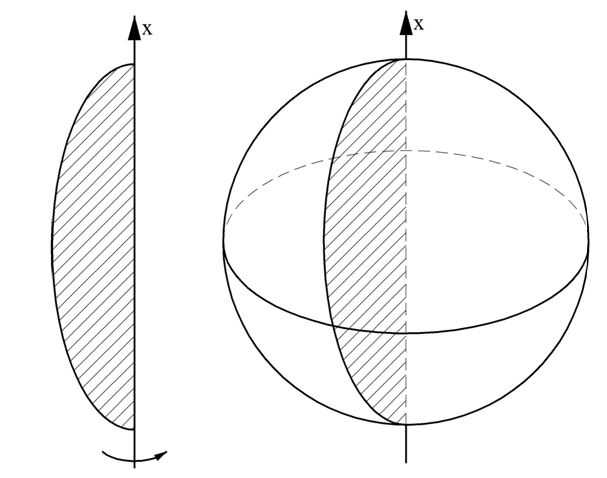
Шар как раз является телом вращения. Он получается при вращении полуокружности вокруг диаметра, на который эта дуга опирается.

Напомним известное нам уравнение окружности, чей центр совпадает с началом координат:

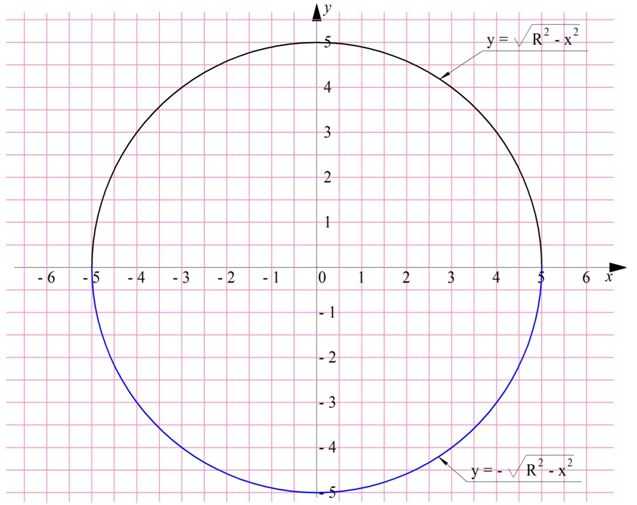
Здесь надо уточнить, что если у получившейся функции впереди записан знак «+», то ее график соответствует полуокружности, находящейся над осью Ох. Если же используется знак «–», то получается уже нижняя полуокружность, расположенная под осью Ох:

В принципе мы можем поворачивать любую из этих полуокружностей вокруг Ох, но мы выберем верхнюю полуокружность. Заметим, что эта дуга начинается в точке х = – R и заканчивается в точке х = R, эти числа будут пределами интегрирования. Тогда объем шара равен:

Задание. Найдите объем шара с радиусом 6.

Решение. Подставляем радиус из условия в формулу:

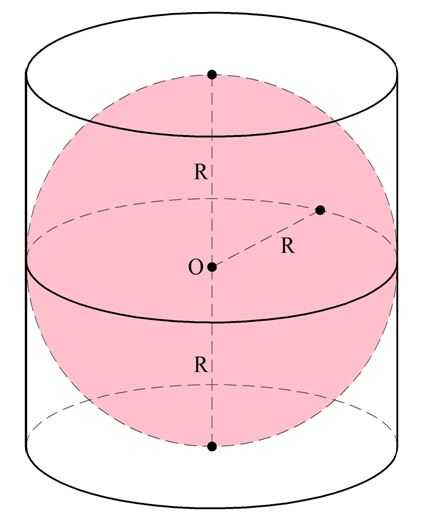
Задание. В цилиндр вписан шар. Во сколько раз объем цилиндра больше объема такого шара?

Решение. Ясно, что так как шар вписан в цилиндр, то радиусы этих тел одинаковы. Обозначим этот радиус как R. Также ясно, что раз шар касается оснований цилиндра, то расстояние между ними (то есть высота цилиндра) равно двум радиусам шара:

Объем пирамиды

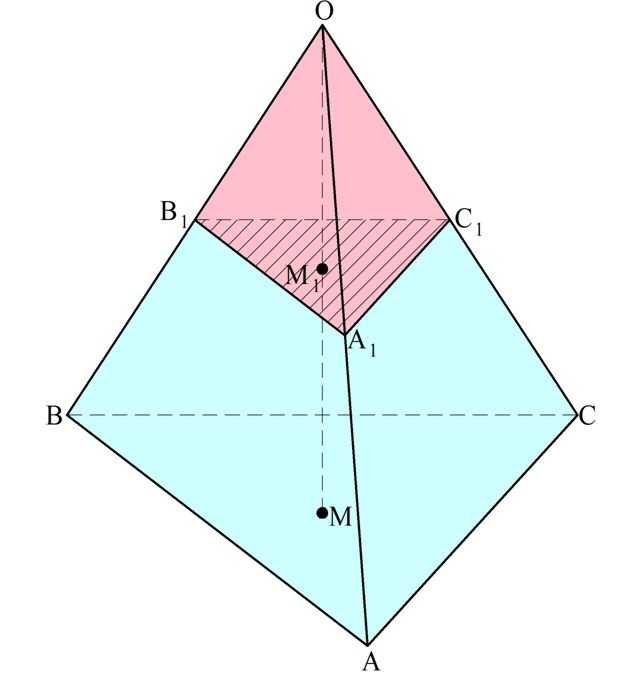
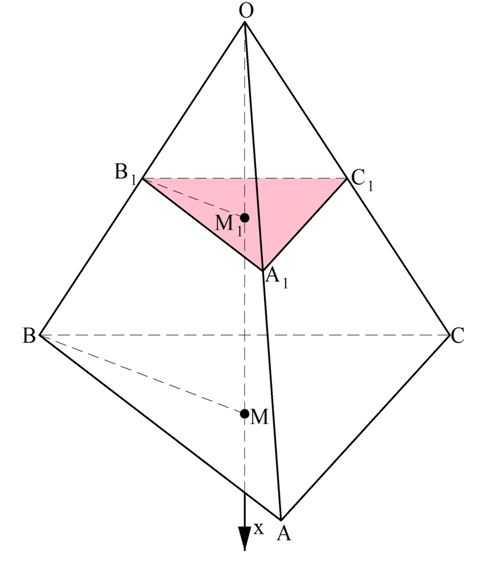
Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.

Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.

Далее построим сечение А₁В₁С₁, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ₁. Тогда ОМ₁ – это координата х, характеризующая расположение сечения А₁В₁С₁.

Осталось составить выражение для площади ∆А₁В₁С₁. Так как АВ||A₁B₁, то ∠АВО и ∠А₁В₁О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А₁В₁О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что

Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ₁В₁. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому

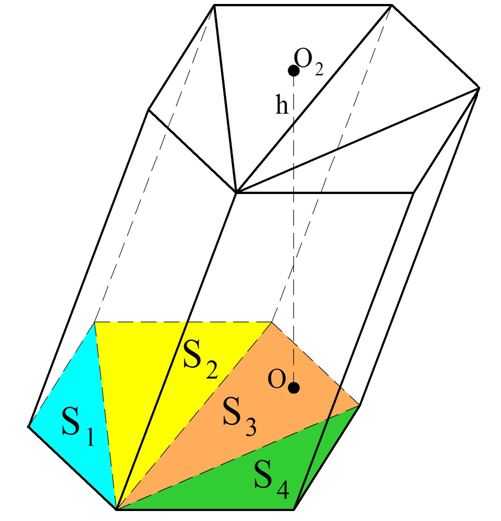
Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:

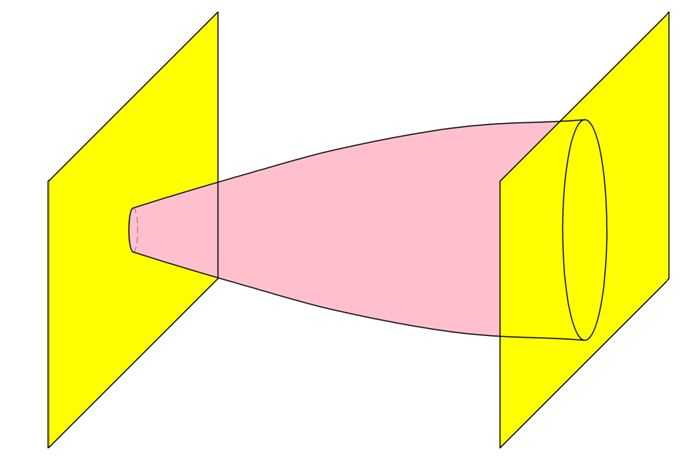
Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S₁, S₂, S₃…, которые в сумме составляют площадь многоугольника S.

Объем треугольных пирамид рассчитывается по выведенной нами формуле:

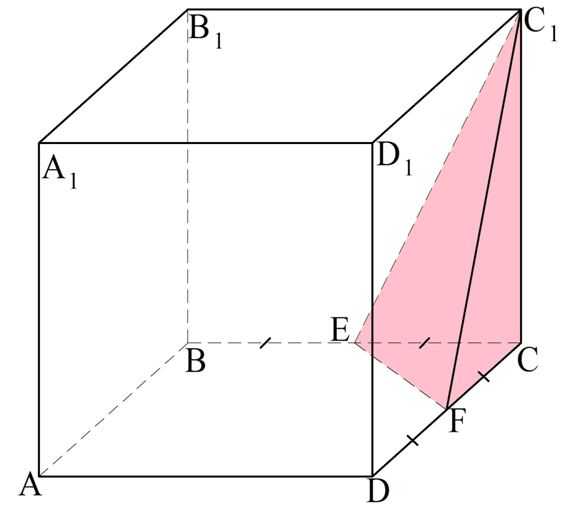
Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.

Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:

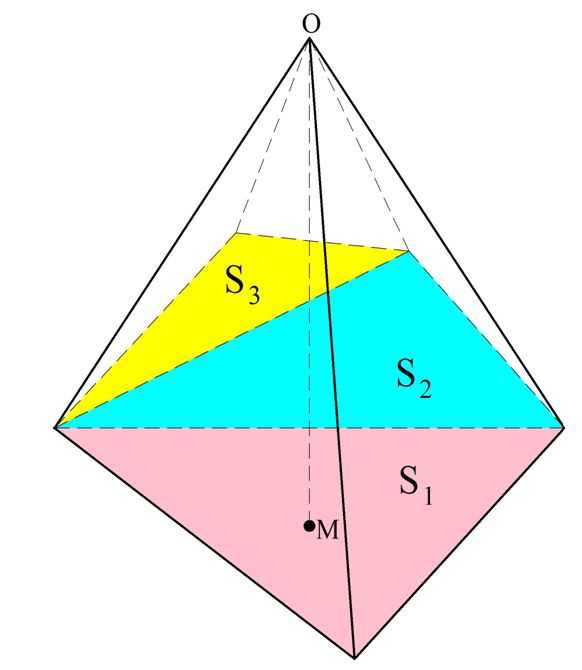
Задание. В кубе АВСDA₁В₁С₁D₁ отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С₁EFC меньше объема куба?

Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:

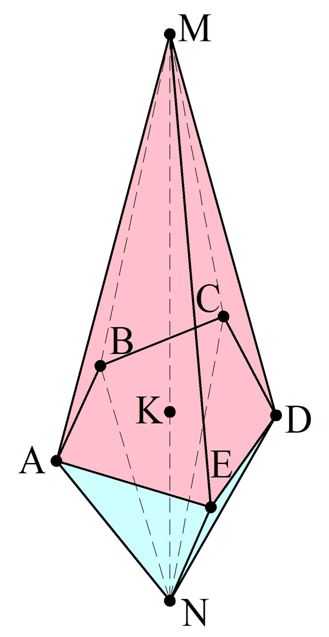
Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?

Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.

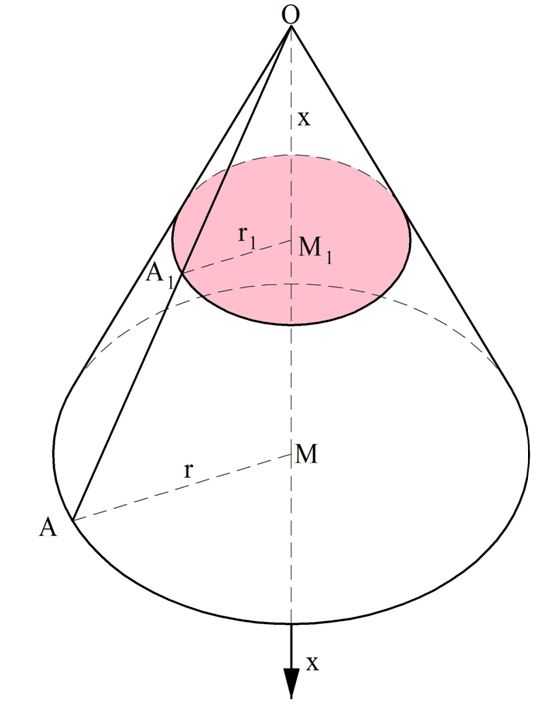
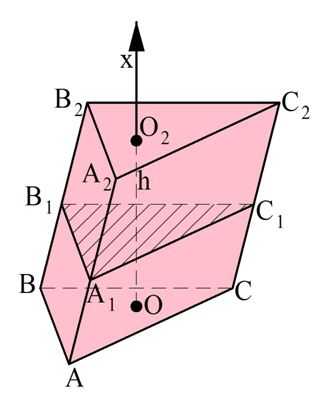
Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.

Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А₁В₁С₁, параллельное основанию.

Обозначим площадь нижнего основания пирамиды как S₂, а площадь верхнего основания – как S₁. Далее высоту усеченной пирамиды (отрезок ММ₁) обозначим как h. Мы уже выяснили ранее, что основания АВС и А₁В₁С₁ – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ₁. Тогда можно записать:

Далее используем основное свойство пропорции:

Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:

Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.

Сначала вычислим площади оснований:

Примеры заданий

Задача первая. Дан куб с ребром 12 см. Вычислить его объем и выразить ответ в квадратных метрах.

В этом задании будет сложнее перевести ответ в другие единицы, чем решить, как найти объем куба. Для выполнения первой части задания потребуется формула, записанная под номером 6. После возведения в куб числа 12 получится ответ 1728 см3. Теперь нужно вспомнить, как перевести их в кубические метры. Для этой цели ответ нужно разделить на 100 три раза. Сотня появилась из того факта, что в одном метре именно сто сантиметров. А деление выполняется трижды, потому что единицы в задании кубические. Итак, 1728 разделенное на 100 даст 17,28. После второго деления получится 0,1728. Третье действие даст ответ 0,001728 м3. Это и есть ответ задачи: объем куба равен 0,001728 м3 .

Задача вторая. Имеется куб с площадью всей его поверхности, равной 600 дм2. Найти объем фигуры и выразить его в кубических метрах.

Для ответа на вопрос этого задания будет нужна формула номер 7. Первым действием известное число делится на 6. В ответе получается 100. Из него легко извлечь квадратный корень, он будет равен 10. Теперь десятку нужно возвести в куб. Так получается, что искомая величина равна 1000 дм3. Осталось перевести его в м3. Как и в предыдущей задаче, деление будет выполняться три раза, только делителем будет 10. Потому что в одном метре десять дециметров. После деления получается ответ равный 1 м3. Ответ: объем равен 1 м3.

Задача третья. Дан куб с длиной диагонали его грани, равной √2 мм. Нужно вычислить объем.

Восьмая формула поможет в том, как найти ответ в этой задаче. Первым делом нужно возвести в куб известную величину. Квадратный корень из 2 в третьей степени даст значение 2√2. После умножения на √2 получится число 4. Последним действием нужно его разделить на 4. Ответ: объем куба 1 мм3.

Задача четвертая. Известно, что диагональ куба равна 3 м. Требуется вычислить его объем.

Будет просто найти ответ на эту задачу по формуле под номером 9. Величину, которая дана в условии, нужно возвести в куб. Получится 27. После его деления на 9 ответ станет равен 3. И последним действием его нужно умножить на квадратный корень из 3. Ответом задачи будет 3√3 м3.

Определение площади поверхности куба.

Определение площади поверхности куба выполняется по формуле SA = 6а2. Куб (правильный гексаэдр) – это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.

Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а2. Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять – a2, где а – сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).

11 Как определить объём сферического изделия

Сферические изделия встречаются в нашей жизни почти каждый день. Это может быть элемент подшипника, футбольный мяч или пишущая часть шариковой ручки. В некоторых случаях нам необходимо узнать, как рассчитать кубатуру сферы для определения количества жидкости в ней.

Как утверждают эксперты, для вычисления объёма этой фигуры используется формула V=4/3ԉr3, где:

• V – подсчитываемый объём детали;
• R- радиус сферы;
• ԉ – постоянная величина, которая равняется 3,14.

Для проведения необходимых вычислений нам нужно взять рулетку, зафиксировать начало измерительной шкалы и провести замер, причём лента рулетки должна проходить по экваторe шара. После этого узнают диаметр детали, поделив размер на число ԉ.

А теперь ознакомимся с конкретным примером вычисления для сферы, если её длина по окружности равняется 2,5 метрам. Сначала определим диаметр 2,5/3,14=0,8 метра. Теперь подставляем это значение в формулу: