Эллипс

Определение и элементы эллипса

Определение. Эллипс — это замкнутая плоская кривая, которая имеет уравнение x²/a²+y²/b²=1. Это каноническое уравнение эллипса, в нем координатные оси совпадают с осями эллипса.

Он имеет два фокуса. Это такие точки, сумма расстояний от которых до любой P(x,y) есть постоянная величина.
Эллипс также можно описать как пересечение плоскости и кругового цилиндра.

Эллипс

Элементы:

• F₁ , F₂ – фокусы . F₁ = ( c ; 0); F ₂ (- c ; 0)
• A₁ A₂ — большая ось;
• B₁ B₂ — малая ось;
• О — центр эллипса (пересечения малой и большой осей);
• A₁, A₂, B₁, B₂ — вершины эллипса;
• Диаметр эллипса — отрезок, соединяющий две точки эллипса и проходящий через O;
• с – фокусное расстояние, половина расстояния между F₁ и F₂;
• a – большая полуось эллипса;
• b – малая полуось;
• r₁ и r₂ — фокальные радиусы эллипса;
• если a > b, то уравнения директрис эллипса x=-a/e, x=a/e;
• если a < b, уравнения директрис y = -b/e, y = b/e;
• Фокальный параметр p = b2/a — отрезок, который соединяет фокус фигуры и точку на кривой, перпендикулярен ее большей оси.

Теорема. Фокусное расстояние c и полуоси эллипса связаны соотношением:

a² = b² + c².

Доказательство: В случае, если М лежит на пересечении кривой с вертикальной осью, r₁ + r₂ = 2*(по теореме Пифагора). В случае, если М — пересечение его с горизонтальной осью, r₁ + r₂ = а – c + а + c. Т.к. по определению сумма r₁ + r ₂ – постоянна, то , приравнивая, получаем:

a² = b² + c²

r₁ + r₂ = 2 а .

Объяснение метода

1. 1

   Вспомните формулу для площади круга. Вероятно, вы помните, что площадь круга равна πr2, то есть π x r x r. Что, если мы попробуем найти площадь круга по формуле для эллипса? В этом случае следует измерить радиус в одном направлении: r. Измерим радиус в перпендикулярном направлении, и тоже получим r. Подставим в формулу для площади эллипса: π x r x r! Таким образом, круг является лишь отдельной разновидностью эллипса.

2. 2

   Представьте, что круг сплющили. Вообразите, что круг сжали до формы эллипса. По мере сжатия один радиус круга будет становиться все короче, а второй — длиннее. При этом площадь круга будет оставаться неизменной, поскольку ничто не покидает его и не добавляется к нему. Если мы используем в формуле для площади короткий и длинный радиусы, то “сплющивание” и “расширение” уравновесят друг друга, и в результате получится правильный ответ.

Как подобрать эллиптический тренажер по длине шага

Во время покупки тренажера необходимо узнать длину шага между педалями. Она прямо пропорциональна росту человека.

Обычно большую длину между педалями имеют профессиональные и дорогие эллипсоиды, но можно найти и приемлемые варианты. Хорошо себя зарекомендовали следующие модели с шагом от 40 до 50 сантиметров:

Если рост занимающегося меньше 170 см, то ему подойдет эллипсоидный тренажёр с расстоянием между педалями 33-40 см. Она считается классической, поэтому можно обойтись недорогим снарядом. В этой категории, на сегодня, популярны следующие модели:

Если же оборудование покупается для нескольких человек, у которых разный рост, то лучше выбрать тренажер с возможностью регулирования длины шага педалей. Тогда каждый занимающийся сможет устанавливать свои параметры.

Особым механизмом регулировки шага педалей оснащены следующие модели эллипсоидов:

Как измерить длину шага

В характеристиках эллиптического тренажёра обычно указаны подобные параметры. Но уточнить информацию возможно самостоятельно. Измерить длину шага у эллипсоида несложно. Для этого существует два способа:

1. Необходимо измерить расстояние от центра оси, на которую крепятся опоры педалей, до середины маховика и умножить получившийся результат на два. Не стоит просто измерять диаметр самого маховика. Значение получится на 3-4 см больше, из-за того, что ось находится дальше от края диска на несколько сантиметров.
2. Педали необходимо зафиксировать на максимальном расстоянии друг от друга. Шаг эллипсоида будет равняться промежутку от начала или середины передней до начала или середины второй.

Длина шага для эллиптического тренажера подбирается исходя из роста человека

Уравнение касательной к эллипсу.

Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть \(M_{0}(x_{0}, y_{0})\) — точка на эллипсе и \(y_{0} \neq 0\). Через \(M_{0}\) проходит график некоторой функции \(y=f(x)\), который целиком лежит на эллипсе. (Для \(y_{0} > 0\) это график \(f_{1}(x)=b\sqrt{1-x^{2}/a^{2}}\), для \(y_{0} < 0\) — график \(f_{2}(x)=-b\sqrt{1-x^{2}/a^{2}}\). Не уточняя знака \(y_{0}\), обозначим подходящую функцию \(f(x)\).) Для нее выполнено тождество
$$
\frac{x^{2}}{a^{2}}+\frac{(f(x))^{2}}{b^{2}}=1.\nonumber
$$
Дифференцируем его по \(x\):
$$
\frac{2x}{a^{2}}+\frac{2ff’}{b^{2}}=0.\nonumber
$$
Подставляя \(x=x_{0}\) и \(f(x_{0}=y_{0})\), находим производную от \(f\) в точке \(x_{0}\), равную угловому коэффициенту касательной:
$$
f'(x_{0})=\frac{b^{2}}{a^{2}} \frac{x_{0}}{y_{0}}.\nonumber
$$
Теперь мы можем написать уравнение касательной:
$$
y-y_{0}=-\frac{b^{2}}{a^{2}} \frac{x_{0}}{y_{0}}(x-x_{0}).\nonumber
$$
Упрощая это уравнение, учтем, что \(b^{2}x_{0}^{2}+a^{2}y_{0}^{2}=a^{2}b^{2}\), так как \(M_{0}\) лежит на эллипсе. Результату можно придать вид
$$
\frac{xx_{0}}{a^{2}}+\frac{yy_{0}}{b^{2}}=1.\label{ref8}
$$

При выводе уравнения \eqref{ref8} мы исключили вершины эллипса \((a, 0)\) и \((-a, 0)\), положив \(y_{0} \neq 0\). Для этих точек оно превращается, соответственно, в уравнения \(x=a\) и \(x=-a\). Эти уравнения определяют касательные в вершинах. Проверить это можно, заметив, что в вершинах ж как функция от у достигает экстремума. Предоставим читателю проделать это подробно и показать тем самым, что уравнение \eqref{ref8} определяет касательную для любой точки \(M_{0}(x_{0}, y_{0})\) на эллипсе.

Утверждение 5.

Касательная к эллипсу в точке \(M_{0}(x_{0}, y_{0})\) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.

Нам надо сравнить углы \(\varphi_{1}\) и \(\varphi_{2}\), составленные векторами \(\overrightarrow{F_{1}M_{0}}\) и \(\overrightarrow{F_{2}M_{0}}\) с вектором \(\boldsymbol{n}\), перпендикулярным касательной (рис. 8.5). Из уравнения \eqref{ref8} находим, что \(\boldsymbol{n}(x_{0}/a^{2}, y_{0}/b^{2})\), и потому
$$
(\overrightarrow{F_{1}M_{0}}, \boldsymbol{n})=\frac{x_{0}}{a^{2}}(x_{0}-c)+\frac{y_{0}}{b^{2}}y_{0}=1-\frac{x_{0}c}{a^{2}}=\frac{a-\varepsilon x_{0}}{a}.\nonumber
$$
Используя \eqref{ref4}, мы получаем отсюда, что \(\cos \varphi_{1}=1/(a|\boldsymbol{n}|)\). Аналогично находим \(\cos \varphi_{2}=1/(a|\boldsymbol{n}|)\). Утверждение доказано.

Рис. 8.5.

Расчет площади

1. 1

   Определите большую полуось эллипса. Это расстояние от центра эллипса до его самого дальнего края. Большую полуось можно представить себе в качестве максимального радиуса эллипса. Измерьте длину большой полуоси или найдите ее значение в условии задачи. Обозначим эту длину буквой a

   Большая полуось эллипса является максимальным расстоянием от его центра до края.

   .

2. 2

   Определите малую полуось эллипса. Как можно догадаться по названию, это кратчайшее расстояние от центра эллипса до его края. Обозначим это расстояние латинской буквой b.

   • Малая полуось эллипса расположена под прямым углом 90º к его большой полуоси, однако для нахождения площади нет необходимости определять углы.
   • Малая полуось эллипса является минимальным расстоянием от его центра до края.

3. 3

   Умножьте на число “пи”. Площадь эллипса равна a x b x π. Поскольку перемножаются две величины с размерностью длины, в ответе получится длина в квадрате.

   • Например, если большая полуось эллипса равна 5 единицам, а малая 3 единицам длины, то получим площадь 5 x 3 x π, или около 47 квадратных единиц длины.
   • Если у вас нет под рукой калькулятора или на калькуляторе нет символа π, используйте вместо этого числа значение “3,14”.

Длина дуги эллипса

Длина дуги плоской линии определяется по формуле:

Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:

После замены выражение для длины дуги принимает окончательный вид:

Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода . В частности, периметр эллипса равен:

,

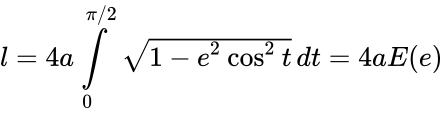где  — полный эллиптический интеграл второго рода.

Приближённые формулы для периметра

Максимальная погрешность этой формулы ~0,63 % при эксцентриситете эллипса ~0,988 (соотношение осей ~1/6,5). Погрешность всегда положительная.

Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:

, где

Максимальная погрешность этой формулы ~0,36 % при эксцентриситете эллипса ~0,980 (соотношение осей ~1/5). Погрешность также всегда положительная.

Существенно лучшую точность при обеспечивает формула Рамануджана:

При эксцентриситете эллипса ~0,980 (соотношение осей ~1/5) погрешность составляет ~0,02 %. Погрешность всегда отрицательная.

Еще точней оказалась вторая формула Рамануджана:

Точные формулы для периметра

Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:

Альтернативная формула

где  — Арифметико-геометрическое среднее 1 и ,
а  — модифицированное арифметико-геометрическое среднее 1 и , которое было введено С. Ф. Адлаем в статье 2012 года.

Как построить эллипс?

Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:

Пример 1

Построить эллипс, заданный уравнением

Решение: сначала приведём уравнение к каноническому виду:

Зачем приводить? Одно из преимуществ канонического уравнения заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению .

В данном случае ::Отрезок называют большой осью эллипса;отрезок называют большой осью эллипса;отрезок – малой осью>;число называют большой полуосью эллипса; число называют большой полуосью эллипса; число – малой полуосью.в нашем примере: .

Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.

Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы. И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.

По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями . Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.

Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса на черновике быстренько выражаем: на черновике быстренько выражаем:

Далее уравнение распадается на две функции: – определяет верхнюю дугу эллипса; – определяет верхнюю дугу эллипса; – определяет нижнюю дугу эллипса.

Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция . Напрашивается нахождение дополнительных точек с абсциссами . Напрашивается нахождение дополнительных точек с абсциссами . Настукаем три смс-ки на калькуляторе:Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.

Отметим на чертеже точки (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию: (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию:Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?

Понятие алгебраической линии и её порядка

Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид , где , где – многочлен, состоящий из слагаемых вида (( – действительное число, – целые неотрицательные числа).

Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательныхстепенях.

Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости

Порядок линии равен максимальному значению входящих в него слагаемых.

По соответствующей теореме, понятие алгебраической линии, а также её порядок не зависят от выбора аффинной системы координат, поэтому для лёгкости бытия считаем, что все последующие выкладки имеют место быть в декартовых координатах .

Общее уравнение линии второго порядка имеет вид , где , где – произвольные действительные числа ( принято записывать с множителем-«двойкой»), причём коэффициенты принято записывать с множителем-«двойкой»), причём коэффициенты не равны одновременно нулю.

Если , то уравнение упрощается до , то уравнение упрощается до , и если коэффициенты одновременно не равны нулю, то это в точности общее уравнение «плоской» прямой, которая представляет собой линию первого порядка.

Многие поняли смысл новых терминов, но, тем не менее, в целях 100%-го усвоения материала сунем пальцы в розетку. Чтобы определить порядок линии, нужно перебрать все слагаемыееё уравнения и у каждого из них найти сумму степенейвходящих переменных.

Например:

слагаемое содержит «икс» в 1-й степени;слагаемое содержит «икс» в 1-й степени;слагаемое содержит «игрек» в 1-й степени;в слагаемом переменные отсутствуют, поэтому сумма их степеней равна нулю.

Далее из полученных чисел выбирается максимальное значение, в данном случае единица, – это и есть порядок линии.

Теперь разберёмся, почему уравнение задаёт линию второго порядка:

слагаемое содержит «икс» во 2-й степени;у слагаемого содержит «икс» во 2-й степени;у слагаемого сумма степеней переменных: 1 + 1 = 2;слагаемое содержит «игрек» во 2-й степени;все остальные слагаемые – меньшей степени.

Максимальное значение: 2

Если к нашему уравнению дополнительно приплюсовать, скажем, , то оно уже будет определять линию третьего порядка. Очевидно, что общий вид уравнения линии 3-го порядка содержит «полный комплект» слагаемых, сумма степеней переменных в которых равна трём:, то оно уже будет определять линию третьего порядка. Очевидно, что общий вид уравнения линии 3-го порядка содержит «полный комплект» слагаемых, сумма степеней переменных в которых равна трём:, где коэффициенты не равны одновременно нулю.

В том случае, если добавить одно или несколько подходящих слагаемых, которые содержат , то речь уже зайдёт о линии 4-го порядка, и т.д.

С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат.

Однако вернёмся к общему уравнению и вспомним его простейшие школьные вариации. В качестве примеров напрашивается парабола и вспомним его простейшие школьные вариации. В качестве примеров напрашивается парабола , уравнение которой легко привести к общему виду , и гипербола , и гипербола с эквивалентным уравнением . Однако не всё так гладко….

Существенный недостаток общего уравнения состоит в том, что почти всегда не понятно, какую линию оно задаёт. Даже в простейшем случае не сразу сообразишь, что это гипербола. Такие расклады хороши только на маскараде, поэтому в курсе аналитической геометрии рассматривается типовая задача приведения уравнения линии 2-го порядка к каноническому виду.

Фокусы, эксценриситет и директрисы эллипса.

У эллипса есть две замечательные точки, которые называются его фокусами.

Определение.

Пусть по определению
$$
c^{2}=a^{2}-b^{2}\label{ref2}
$$
и \(c \geq 0\).

Фокусами называются точки \(F_{1}\) и \(F_{2}\) с координатами \((c, 0)\) и \((-c, 0)\) в канонической системе координат (рис. 8.3).

Рис. 8.3. Фокусы эллипса.

Для окружности \(c=0\), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.

Определение.

Отношение
$$
\varepsilon=\frac{c}{a}\label{ref3}
$$
называется эксцентриситетом эллипса.

Отметим, что \(\varepsilon < 1\).

Утверждение 2.

Расстояние от произвольной точки \(M(x, y)\), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы \(x\):
$$
r_{1}=|F_{1}M|=a-\varepsilon x,\ r_{2}=|F_{2}M|=a+\varepsilon x.\label{ref4}
$$

Очевидно, что \(r_{1}^{2}=(x-c)^{2}+y^{2}\). Подставим сюда выражение для \(y^{2}\), найденное из уравнения эллипса. Мы получим
$$
r_{1}^{2}=x^{2}-2cx+c^{2}+b^{2}-\frac{b^{2}x^{2}}{a^{2}}.\nonumber
$$

Учитывая равенство \eqref{ref2}, это можно преобразовать к виду
$$
r_{1}^{2}=a^{2}-2cx+\frac{c^{2}x^{2}}{a^{2}}=(a-\varepsilon x)^{2}.\nonumber
$$
Так как \(x \leq a\) и \(\varepsilon < 1\), отсюда следует, что справедливо первое из равенств \eqref{ref4}: \(r_{1}=a-\varepsilon x\). Второе равенство доказывается аналогично.

Утверждение 3.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса \(2a\).

Необходимость. Если мы сложим равенства \eqref{ref4} почленно, то увидим, что
$$
r_{1}+r_{2}=2a.\label{ref5}
$$Достаточность. Пусть для точки \(M(x, y)\) выполнено условие \eqref{ref5}, то есть
$$
\sqrt{(x-c)^{2}+y^{2}}=2a-\sqrt{(x+c)^{2}+y^{2}}.\nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^{2}=a\sqrt{(x+c)^{2}+y^{2}}.\label{ref6}
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение \eqref{ref2}. Мы придем к \(b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}\), равносильному уравнению эллипса \eqref{ref1}.

С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе координат (рис. 8.4)
$$
x=\frac{a}{\varepsilon},\\ x=-\frac{a}{\varepsilon}.\label{ref7}
$$
Директрису и фокус, которые лежат по одну сторону от центра, будем считать соответствующими друг другу.

Рис. 8.4. Фокусы и директрисы эллипса.

Утверждение 4.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса \(\varepsilon\).

Докажем это предложение для фокуса \(F_{2}(-c, 0)\). Пусть \(M(x, y)\) — произвольная точка эллипса. Расстояние от \(M\) до директрисы с уравнением \(x=-a/\varepsilon\) по формуле (9) §3 гл. II равно
$$
d_{2}=|x+\frac{a}{\varepsilon}|=\frac{1}{\varepsilon}(\varepsilon x+a).\nonumber
$$
Из формулы \eqref{ref4} мы видим теперь, что \(r_{2}/d_{2}=\varepsilon\).

Обратно, пусть для какой-то точки плоскости \(r_{2}/d_{2}=\varepsilon\), то есть
$$
\sqrt{(x+c)^{2}+y^{2}}=\varepsilon \left(x+\frac{a}{\varepsilon}\right).\nonumber
$$
Так как \(\varepsilon=c/a\), это равенство легко приводится к виду \eqref{ref6}, из которого, как мы знаем, следует уравнение эллипса.

Что такое Q-фактор эллиптического тренажера

Еще одним важным параметром, на который нужно обращать внимание при выборе эллипсоида, будет Q-фактор. Этот показатель является расстоянием между педалями, то есть шириной шага

Он необходим для комфортных и продуктивных занятий. Чем ширина между педалями эллипсоида ближе к естественному положению ног, тем удобнее заниматься. Неправильное расстояние будет давать лишнюю нагрузку на тазобедренный сустав. Подбирается Q-фактор в эллиптическом тренажёре в зависимости от роста человека и индивидуальных особенностей. Например, на моделях с задним приводом значение этого параметра будет около 20 см, то есть расстояние ног на ширине плеч. Если рост занимающегося ниже 165, то тренироваться на таком снаряде будет крайне неудобно. К тренажерам с задним расположением вала можно отнести например Эллиптический тренажер CardioPower E200.

CardioPower E410

Полезные советы

Измерить Q-фактор эллипсоида довольно просто. Для это просто проверяют ширину между педалями, от края одной до края второй. Хотя подобные параметры указаны в характеристиках снаряда.

Чтобы найти эффективное и комфортное устройство, необходимо пробовать. Лучше всего вставать на педали эллипсоидного тренажера, делать пару легкий движений. Если во время пробных упражнений не ощущается дискомфорта и напряжения в области таза и коленей, то снаряд подходит идеально. В течение тренировки усилие должно приходиться только на мышцы, а не суставы. Длина шага и Q-фактор являются ключевыми характеристиками при подборе эллипсоида. Именно благодаря им занимающийся будет, или не будет, получать нужную нагрузку. Неправильное соотношение этих показателей снижает эффективность тренировок, а также способно привести к травмам. Теперь вы знаете, как выбрать эллиптический тренажер по длине шага и Q-фактору. Но помните, что эксперты советуют лично «примерять» тренажер, потому-что только так возможно найти именно «свою» модель.

Решение задач на эллипс

Соберем все формулы вместе:

1. — каноническое уравнение эллипса;
2. координаты левого фокуса F₁(-c,0), правого F₂(c,0);
3. связь а, b, с  a² = b² + c²
4. e = c/а эксцентриситет;
5. фокальные радиусы r₁ = a + ex, r₂ = a — ex;
6. директрисы x = -a/e, x = a/e;
7. расстояние между директрисами 2a/e;
8. Площадь эллипса S = πab.

Пример 1. Составить уравнение прямой, проходящей через F₁ и нижнюю вершину линии эллипс:

Решение:

• Координаты нижней вершины: x = 0; y2 = 16; y = -4.
• Координаты фокуса: с² = а² – b² = 25 – 16 = 9; с = 3; F₁ (-3; 0).
• Прямая, проходящей через две точки:

Пример 2. Дана кривая 9×2 + 25y2 = 225. Найти: 1) показать, что это эллипс, найти его полуоси 2) эксцентриситет 3) директрисы.

Решение:

Разделим обе стороны на 225

сократим, получим каноническое уравнение эллипса

Следовательно, 1) полуоси a = 5, b = 3, 2) F₁(-c, 0), F₂(c, 0) с определим из равенства b2 = a2 — c2,  c2 = a2 — b2= 25 — 9 = 16,  c = 4, поэтому  левый фокус F₁(-4, 0), правый F₂(4, 0).

3) e = c/a=4/5.

4) уравнение директрис x = ±a/e =±5*5/4=±25/4.

Пример 3. Эксцентриситет e = 1/3, центр его совпадает с началом координат, F₁ (-2;0). Вычислить расстояние от точки M₁ с абсциссой, равной 2, до директрисы, односторонней с данным фокусом.

Решение:

Т.к. F₁ (-2;0), то с = 2. Зная с и e = 1/3, определим а. e = c/a, а = c/е = 2*3=6. Уравнение директрисы x = -а/e = -6*3 = -18. Точка M₁ имеет координату х = 2. Следовательно, d = |-18|+2=20.

Пример 4. Определить точки эллипса x2/100+y2/36 =1, расстояние от которых до F₂ равно 14. Найти директрисы.

Решение:

a = 10, b = 6, c2 = а2 — b2 = 100 -36 = 64 = 82. Найдем эксцентриситет е = c/а = 8/10 = 4/5. Используем формулу для r₂ = а — еx, 14 = 10 — 4/5*x, отсюда х = -5. Подставим в исходное координату х и найдем у = ±√27 = ±3√3. Условиям задачи удовлетворяют точки (-5; 3√3) и (-5; -3√3).
Уравнения директрис x = ±a/e = ±10/4/5 = ±25/2 = ±12,5.

✦Эллипс 
  ✦Фокус F₁, F₂ 
  ✦Уравнение эллипса 
  ✦Малая полуось 
  ✦Большая полуось 
  ✦Эксцентриситет 
  ✦Каноническое уравнение 
  ✦Формулы 
  ✦Свойства 
  ✦Малая ось 
  ✦Большая ось 
  ✦Центр 
  ✦Расстояние 
  ✦Радиус 
  ✦Точки 
  ✦Директрисы 
  ✦Коническое сечение 

Автор статьи Степанов Владимир

Что такое длина шага эллиптического тренажёра

Длина шага на эллиптическом тренажёре представляет собой расстояние между педалями во время упражнения, то есть как далеко расходятся ноги при занятии на снаряде. Она показывает широту и правильность амплитуды движений. Наиболее результативным на эллипсоиде считается длина шага от 35 см.

Этот показатель подбирается в зависимости от роста человека. Если выбирать не подходящую ширину шага, то занимающий не сможет проработать все мышцы и получить необходимую нагрузку. Либо во время тренировки человек слишком устанет. Постоянная борьба за комфорт утомляет и снижает желание заниматься.