Что такое парабола

Квадратичная функция

Функция, заданная формулой y=ax2+bx+c, где х,у – переменные, а a,b,c – заданные числа, причем a≠0, называется квадратичной.

Например:

y=2×2+3x+1;  y=0,5×2;    y=-5×2+4x-2;   y=4×2+3.

Графиком квадратичной функции является парабола.

Если a>0, то ветви параболы направлены вверх; если a0: Е=[-D/(4a); +∞);

если a0: минимальное значение равно -D/(4a), максимального значения не существует;

если a0

и D>0: функция положительна (-∞; х1) U (x2; +∞); функция отрицательна – (x1; x2);

и D=0: функция положительна (-∞; х1) U (x1; +∞);

и D-4; n>-4 : 72; n>-1/18.Ответ: (-1/18; +∞).15. Вершина параболы – единственная точка пересечения параболы и прямой. Задайте эту прямую (или прямые, если их несколько) формулой. а) y=-8×2+4x-6;  б) y=6×2-2x+4.

Решение:а) y=-8×2+4x-6.1. Т.к. прямая имеет с параболой единственную точку пересечения, то они могут пересекаться в вершине параболы. Найдем координату у вершины: 

Прямая параллельна оси ОХ и уравнение прямой у=5,5.

2. Также прямая может быть параллельна оси ОУ, уравнение такой прямой х=-b/(2а)=0,25

Все остальные прямые будут иметь две точки пересечения, либо не иметь их вообще.Ответ: у=5,5 и х=0,25.

Задания для самостоятельного решения

1. Из функций выберите квадратичные функции:

у=2×2-3x;  y=(x-1)2-4;   y=3x+2;   y=3×2;   y=x2+3×3-8;  y=x2.

2. Принадлежит ли точка с координатами (1; 0) графику функции у=2×2-3x+1?

3. Найдите абсциссы ( х ) точек пересечения графиков функций  у=0,5×2-1 и у=2х+0,5.

4. Укажите координаты вершины параболы:а) y=2×2+3x+1;   б) y=-x2+4x-5.

5. Найдите промежутки возрастания иубывания функции  y=6×2-13x-5.

6. Постройте график функции y=-(x-2)2-1;  и укажите промежутки знакопостоянства функции.

7. Найдите координаты точек пересечения параболы  y=-4×2+x-1;с прямой у=-4.

8. Найдите нули функции:

9. Задайте формулой квадратичную функцию, график которой изображен на рисунке:

10. Графики функций  y=x2+bx+c и у=2х-3 пересекаются в точке с абсциссой 1, а один из нулей функции y=x2+bx+c равен 2. Найдите c и b.

Неравенством с одной переменной называется запись, в которой два выражения, содержащие одну и ту же переменную связаны знаками неравенств: , ≥, ≤, ≠.

Решением неравенства называется такое числовое значение переменной, при подстановке которого в данное неравенство оно становится верным числовым неравенством.

Решить неравенство с переменной – значит найти все его решения или доказать, что их нет.

Два неравенства с одной переменной называются равносильными, если решения этих неравенств совпадают.

1. Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится неравенство, равносильное данному. 2. Если к обеим частям неравенства с одной переменной прибавить или вычесть одно и то же число, то получится неравенство, равносильное данному.3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное данному.

Линейным неравенством называется неравенство вида ax > b (либо ax

Если a>0, то неравенство ax>0  равносильно неравенству x>b:a, значит, множество решений неравенства есть промежуток .

Если abравносильно неравенству xb  принимает вид 0x>b, т.е. оно не имеет решений, если b

≥0, и верно при любых х, если b0  (либо ax2+bx+c0. В зависимости от знака дискриминанта D=b2-4ac  могут представиться три случая:

1. D0  лежит выше оси, то решением является (-∞; +∞), если a0,  график пересекает ось ОХ в двух точках х1 и х2 (х10, то ветви графика направлены вверх и решением является: (-∞; x1)U(x2;+∞), если a0, то ветви графика направлены вверх и решением является: (-∞; x1)U(x1;+∞), если a0 и A*B>0 (А:B7.

Решение:

а) Из неравенства |x|≤7 следует, что -7≤ х ≤7  и множество решений изображено на рисунке а).

Ответ: а

2. а) Являются ли решениями неравенства 3 – 2(m+6)>-7 + 3(m-4) числа 10; 27; 1,5; -3.

    б) Являются ли решениями неравенства n>-6(3-n)+5(2+n) числа -3; 0,9; 0,5; 1?

Решение:

а) Найдем решение для неравенства 3 – 2(m+6)>-7 + 3(m-4), ля этого раскроем скобки и приведем подобные слагаемые: 

3-2m-12>-7+3m-12;

-5m>-10;

m2, то оно положительное, получим: 66:2; a>2, следовательно утверждение верно.

Ответ: верно

4. При каких значениях х верно неравенство:

а) (2x-5)2≤0;  б) (4x-2)2>0?

Решение:

а) Рассмотрим неравенство (2x-5)2≤0, квадрат числа не может быть отрицательным числом, следовательно рассмотрим случай, когда (2x-5)2=0; 2х-5=0; х=2,5.

 Ответ: 2,5

5. Найдите наименьшее целое решение неравенства:

а) 3х+15

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Примеры решения задач

Задача №1

Найти вершину параболы для уравнения: \(y=x^2-5x+7.\)

Решение: В выражение \(x=-\frac b{2a}\) подставляем известные числа и получаем \(x=\frac52=2,5\). Теперь подставляем x в исходное уравнение: \(2,5^2-5\times2,5+7=0,75.\)

Ответ: (2,5; 0,75).

Задача №2

Найти ВП для уравнения: y=5(x-1)(x+7).

Решение: Ищем нули функции: 5(x-1)(x+7)=0. Тогда x-1=0 либо x+7=0. Из этого x=1; x=-7.

Подставляем и получаем: \(x_0=\frac{x_1+x_2}2=\frac{1+\left(-7\right)}2=-3.\)

Второе: \(y_0=5\times\left(-3-1\right)\left(-3+7\right)=-80.\)

Ответ: (-3; -80). 

Задача №3

Найти вершину параболы для уравнения: \(y=x^2-7x+3 \).

Решение: \(х_0=-\frac b{2a}=-\frac{\left(-7\right)}{2\times1}=3,5.\)

Второе: \(y_0=3,5^2-7\times3,5+3=-9,25.\)

Квадратичная функция — коротко о главном

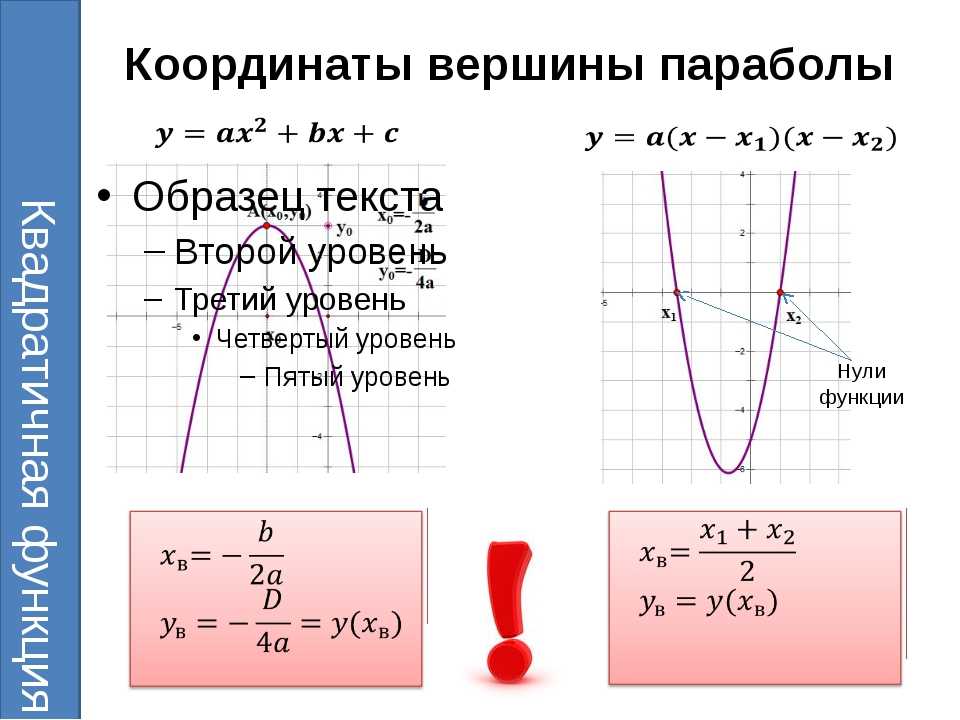
График квадратичной функции – парабола.Вершина параболы: \( \displaystyle {{x}_{в}}=\frac{-b}{2a}\).

Квадратичная функция вида: \( y=a{{x}^{2}}\).

Если коэффициент \( \displaystyle \mathbf{a}<\mathbf{0}\), ветви параболы направлены вниз, если \( \displaystyle \mathbf{a}>\mathbf{0}\) — ветви параболы направлены вверх.

Чем больше значение \( \displaystyle a\) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше \( \displaystyle a\), тем парабола шире.

Варианты расположения параболы в зависимости от коэффициента \( \displaystyle a\) и дискриминанта \( \displaystyle D={{b}^{2}}-4ac\).

Алгоритм построения графика квадратичной функции — параболы:

Три типичных случая построения параболы

Cлучай 1. \( a=-1\).

То есть функция выглядит как \( y=-{{x}^{2}}\). Ну что же здесь сложного? Просто переворачиваем параболу рогами вниз, и все. То есть, теперь будем двигаться так:

• \( 1\) вправо – \( 1\) вниз
• \( 1\) вправо – \( 3\) вниз
• \( 1\) вправо – \( 5\) вниз и т. д.

И то же самое, только влево.

Случай 2. \( a>1\).

Что делать, если, например, \( a=2\)?

Все просто: начинаем так же: \( 1\) вправо, но когда дело доходит до «вверх», любое число увеличиваем в \( 2\) раза:

• \( 1\) вправо – \( 2\) вверх
• \( 1\) вправо – \( 6\) вверх
• \( 1\) вправо – \( 10\) вверх и т. д.

Аналогично в случае \( a<-1\):

• \( 1\) вправо – \( 2\) вниз
• \( 1\) вправо – \( 6\) вниз
• \( 1\) вправо – \( 10\) вниз и т. д.

В общем случае так:

• \( 1\) вправо – \( a\) вверх
• \( 1\) вправо – \( 3a\) вверх
• \( 1\) вправо – \( 5a\) вверх и т. д.

Если \( a<0\), то вместо «вверх» делаем «вниз».

Случай 3. А если \( -1<a<1\)?

Принцип тот же: каждый шаг вправо или влево сопровождается шагом вверх или вниз, равным какому-то нечетному числу, умноженному на \( a\).

Но отмерять нецелые (дробные) отрезки всегда лень. Поэтому иногда удобнее сделать по-другому: шаг вправо или влево делать не \( 1\), а \( \frac{1}{a}\).

Тогда вверх/вниз придется смещаться на целые \( \frac{1}{a}\), \( \frac{3}{a}\), \( \frac{5}{a}\), \( \frac{7}{a}\), … клеток.

Например: построим график \( y=-\frac{1}{3}{{x}^{2}}\). Будем откладывать:

• вправо \( 3\) – вниз \( 3\)
• вправо \( 3\) – вниз \( 9\)
• вправо \( 3\) – вниз \( 15\) и т. д.

и затем то же самое влево.

Что такое функция?

Не знаешь? Тогда сперва прочитай тему «Функции» – она несложная, но очень важная.

А мы пока повторим.

Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).

То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).

Что значит «допустимому»? Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции».

Все дело в понятии «область определения»:

Для некоторых функций не все аргументы можно подставить в зависимость.

Например, для функции \( y=\sqrt{x}\) отрицательные значения аргумента \( x\) – недопустимы.

Кстати, а с линейной функцией ты уже дружишь? Про нее все написано в теме «Линейная функция» – там ты поймешь, что в функциях ничего страшного нет и научишься понимать и использовать коэффициенты (это циферки перед буквой \( x\)).

И еще, надеюсь, ты умеешь решать квадратные уравнения? Освежить память можно, почитав тему «Квадратные уравнения».

Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике

Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)

Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.

Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики. На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях). Мы рассмотрим: 

• степенную функцию (линейную, квадратичную, обратную зависимость, корни), 
• тригонометрические и обратные тригонометрические, 
• показательную и 
• логарифмическую функции.

Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)

Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль? 

Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?

 Можно! И на этом уроке мы научимся производить такие трансформации. 

Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.

Квадратичная функция — подробнее

Число \( a\) называют старшим или первым коэффициентом такой функции, \( b\) – вторым коэффициентом, а \( c\) – свободным членом.

Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений\( E\left( y \right)\).

Какими могут быть значения аргумента квадратичной функции \( y=a{{x}^{2}}+bx+c\)? Правильно, любыми. Ведь в эту формулу можно подставить любое число (в отличии, например, от функции \( y=\frac{1}{x}\) – в нее нельзя подставить \( x=0\)).

Значит, область определения – все действительные числа:

\( D\left( y \right)=\mathbb{R}\) или \( D\left( y \right)=\left( -\infty ;+\infty \right)\).

А теперь множество значений. Все ли значения может принимать функция?

Достаточно рассмотреть самую простую квадратичную функцию \( y={{x}^{2}}\) \( \left( a=1,\text{ }b=0,\text{ }c=0 \right)~\), чтобы убедиться в обратном: ведь какое бы число мы не возводили в квадрат, результат всегда будет больше или равен нулю.

Значит, эта функция всегда не меньше нуля.

А вот больше нуля она может быть сколько угодно: ведь бесконечно большой x в квадрате будет еще больше.

Таким образом, можем написать для \( y={{x}^{2}}:E\left( y \right)=\left[ 0;+\infty \right)\).

Построение квадратичной функции

Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

a — старший коэффициент, который отвечает за ширину параболы. Большое значение a — парабола узкая, небольшое — парабола широкая. b — второй коэффициент, который отвечает за смещение параболы от центра координат. с — свободный член, который соответствует координате пересечения параболы с осью ординат.

График квадратичной функции — парабола, которая имеет следующий вид для y = x2:

 

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:

x	-2	-1	1	2
y	4	1	1	4

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.

График функции y = –x2 выглядит, как перевернутая парабола:

 

Зафиксируем координаты базовых точек в таблице:

x	-2	-1	1	2
y	-4	-1	-1	-4

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.

Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.

Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.

Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1.  Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:



Если a > 0, то график выглядит как-то так:

 

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

 

Выделение полного квадрата

Напомню, что мы можем представить функцию \( y=a{{x}^{2}}+bx+c\) в таком виде:

\( y=a{{\left( x-p \right)}^{2}}+q\).

Например: \( y={{x}^{2}}-6x+5={{\left( x-3 \right)}^{2}}-4\).

Или: \( 2{{x}^{2}}+6x+1=2{{\left( x+1,5 \right)}^{2}}-3,5\).

Что это нам дает?

Дело в том, что число, которое вычитается из \( \displaystyle x\) в скобках (\( \displaystyle p\)) – это абсцисса вершины параболы, а слагаемое за скобками (\( \displaystyle q\)) – ордината вершины.

Это значит, что, построив параболу \( y=a{{x}^{2}}\), нужно будет просто сместить ось \( \displaystyle Oy\) на \( \displaystyle p\) влево и ось \( \displaystyle Ox\) на \( q\) вниз.

Пример: построим график функции \( y=0,5{{x}^{2}}+2x+1\).

Выделим полный квадрат:

\( y=0,5\left( {{x}^{2}}+4x \right)+1=0,5\left( {{x}^{2}}+4x+4-4 \right)+1=0,5\left( {{x}^{2}}+4x+4 \right)-2+1=0,5{{\left( x+2 \right)}^{2}}-1\)Какое число вычитается из \( \displaystyle x\) в скобках? Это \( \displaystyle -2\) (а не \( \displaystyle 2\), как можно решить, не подумав).

Итак, строим параболу \( y=0,5{{x}^{2}}\):

Теперь смещаем ось \( \displaystyle Ox\) на \( \displaystyle -1\) вниз, то есть на \( \displaystyle 1\) вверх:

А теперь – \( \displaystyle Oy\) на \( \displaystyle -2\) влево, то есть на \( \displaystyle 2\) вправо:

Вот и все. Это то же самое, как переместить параболу \( y=0,5{{x}^{2}}\) вершиной из начала координат в точку \( \displaystyle (-2;-1)\), только прямые оси двигать намного легче, чем кривую параболу.

Расчет коэффициентов и основных точек параболы

К числу основных параметров принято относить расположение вершины на оси абсцисс, координаты вершины на оси ординат, параметр директрисы.

Численное значение координаты вершины на оси абсцисс

Если уравнение параболы задано в классическом виде (1), то значение абсциссы в искомой точке будет равняться половине значения параметра s (половине расстояния между директрисой и фокусом). В случае, если функция представлена в виде (2), то x нулевое рассчитывается по формуле:

(3).

Т.е., глядя на эту формулу, можно утверждать, что вершина будет находиться в правой половине относительно оси y в том случае, если один из параметров a или b будет меньше нуля.

Уравнение директрисы определяется следующим уравнением:

(4).

Значение вершины на оси ординат

Численное значение местонахождения вершины для формулы (2) на оси ординат можно найти по такой формуле:

.

Отсюда можно сделать вывод, что в случае если а&lt,0, то вершина кривой будет находиться в верхней полуплоскости, в противном случае – в нижней. При этом точки параболы будут обладать теми же свойствами, что были упомянуты ранее.

Если дана классическая форма записи, то более рациональным будет вычисление значения расположения вершины на оси абсцисс, а через него и последующее значение ординаты. Отметим, что для формы записи (2), ось симметрии параболы, в классическом представлении, будет совпадать с осью ординат.

Важно! При решении заданий с использованием уравнения параболы прежде всего выделите основные значения, которые уже известны. Более того, нелишним будет, если будут определены недостающие параметры

Такой подход заранее даст большее «пространство для маневра» и более рациональное решение. На практике старайтесь использовать запись (2). Она более проста для восприятия (не придется «переворачивать координаты Декарта), к тому же подавляющее количество заданий приспособлено именно под такую форму записи.

Вывод формулы координат вершины параболы

Рассматриваемую формулу используют для решения квадратных уравнений, которые имеют вид:

\(y\;=\;ax^2\;+\;bx\;+\;c\)

Ее график представляет собой параболу, формулу которой мы определили выше. Но не всегда требуется пользоваться данной формулой, так как сначала можно найти значение х, а затем подставить его в уравнение и найти y. 

Для того, чтобы вывести формулу ВП, нужно преобразовать квадратную функцию к виду:

\(y\;=\;f(x\;+\;l)\;+\;m\)

Делают это с помощью метода выделения полного квадрата, то есть \(\left(a+b\right)^2\) преобразуют в \(a^2+2ab+b^2.\)

Функции вида \(y\;=\;f(x\;+\;l)\;+\;m\) отличаются от \(y\;=\;f(x)\) сдвигом из графиков по оси абсцисс на –l и по оси ординат на m. l в переписанной квадратичной функции равняется:

\(\frac{-b}{2a}, а \frac{\left(4ac-b^2\right)}{4a}\)

Получается, что l и m — это координаты x и y.

Приведем доказательство:

1. Соединяем первые два члена многочлена: \(y\;=\;(ax^2\;+\;bx)\;+\;c.\)
2. Выносим коэффициент a за скобку, b при этом делим на a: \(y=a\left(x^2+\frac bax\right)+c.\)
3. Представляем, что у нас есть квадрат суммы, в котором x является слагаемым, а из выражения в скобках необходимо рассчитать его полный квадрат суммы. Одночлен \(\frac bax\) умножаем на два и делим на два одновременно. Далее прибавляем и вычитаем квадрат второго слагаемого квадрата суммы. Получаем: \(y=a\left(x^2+2\frac b{2a}x+\frac{b^2}{4a^2}-\frac{b^2}{4a^2}\right)+c.\)
4. Выделяем квадрат суммы: \(y=a\left(\left(x+\frac b{2a}\right)^2-\frac{b^2}{4a}\right)+c.\)
5. Умножаем на a: \(y=a\left(x+\frac b{2a}\right)^2-\frac{b^2}{4a}+c.\)
6. Приводим свободные члены к общему знаменателю: \(y=a\left(x+\frac b{2a}\right)^2-\frac{b^2+4ac}{4a}.\)
7. Меняем знак: \(y=a\left(x+\frac b{2a}\right)^2+\frac{b^2-4ac}{4a}.\)

Мы привели функцию \(y\;=\;ax^2\;+\;bx\;+\;c\) к виду \(y\;=\;a{(x\;+\;l)}^2\;+\;m,\) что соответствует \(y\;=\;f(x\;+\;l)\;+\;m,\) где \(f(x)\;=\;ax^2. \)